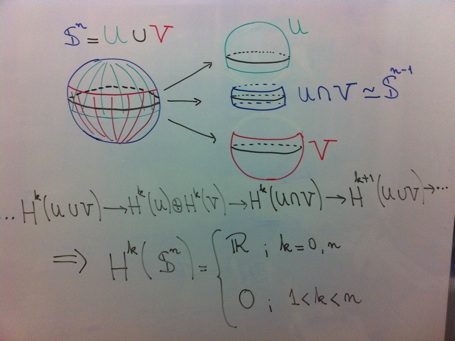Variedades Diferenciáveis

Descrição: Essencialmente, uma variedade diferenciável é um espaço topológico onde é possível calcular derivadas de funções reais. Esta disciplina consiste num estudo geométrico e topológico de variedades diferenciáveis. Também faremos uso de ferramentas algébricas para entender a topologia de uma variedade diferenciável e veremos como, em determinadas situações, a topologia impede a existência de certas estruturas geométricas. Não é assumido nenhum conhecimento prévio sobre variedades diferenciáveis, porém, um bom conhecimento de topologia é recomendável.
Aulas: Terças e Quintas 15:30-17:30 no Anfiteatro B do Centro Politécnico
Avaliação: Listas de exercícios (L), uma prova (P) e projeto final (PF). A nota final será calculada assim:
Nota Final= 0,5 x L + 0,25 x P + 0,25 x PF
Projetos Finais:
-
-Fernando de Ávila: Teorema de estabilidade de Reeb local
-
-Fernando Studzinski: Conexões e curvatura em fibrados principais
-
-Dion Ross: Complexos diferenciais associados a EDP’s
Ementa: Os tópicos que estudaremos neste curso são:
Parte 1: Variedades Diferenciáveis
-
1. Definição de variedade diferenciável e exemplos.
-
2. Aplicações diferenciáveis
-
3. Variedades com bordo, cobordismo
-
4. Fibrado tangente e campos de vetores
-
5. Distribuições e Teorema de Frobenius: conceito de folheação regular
-
6. Transversalidade; Teorema de Withney e Interseção
Parte 2: Formas Diferenciais
-
1. Tensores
-
2. Fibrado exterior de uma variedade diferenciável
-
3. Definição de formas diferenciais; exemplos e representação local
-
4. Derivada exterior
-
5. Integração
-
6. Teorema de Stokes
-
7. Lema de Poincaré
-
8. Grupos de cohomologia de De Rham
-
9. Sequência de Mayer Vietoris; cálculo explícito de grupos de cohomologia
-
10. Dualidade de Poincaré
-
11. Fórmula de Künneth
Parte 3: Aplicações
Dependendo do interesse dos alunos, algumas aplicações possíveis incluem:
-
1. Noções básicas de grupos de Lie; exemplos, cohomologia de grupos de Lie.
-
2. Fibrados vetoriais e conexões; classes características
-
3. Teoria de Morse
-
4. Operador estrela de Hodge
-
5. e mais...
Referências: A literatura sobre o assunto é extensa. Sugerimos os seguintes textos:
-
• R. Bott, L. Tu, Differential forms in algebraic topology, Springer Verlag
-
• H. Cartan, Differential forms, Dover
-
• J. Lee, Introduction to smooth manifolds, Springer Verlag
-
• M. Spivak, A comprehensive introduction to differential geometry, Publish or Perish INC, Edição 3
Listas:
-
• Lista1 (Para ser entregue dia 28 de março em aula)
-
• Lista2 (Para ser entregue dia 03 de maio)
-
• Lista 3 (Para ser entregue dia 14 de junho)
-
• Lista4: A lista 4 consiste em entregar o exercício proposto em aula sobre obstruções cohomológicas para uma variedade ser “null cobordant”.