9. Geometria e Programação Geométrica

Vamos interromper nossa apresentação sobre WebGL para revisar alguns fundamentos de geometria necessários para o resto do curso. Além da CG, há diversas outras áreas da Computação que envolvem entidades geométricas, como CAD (computer aided design), visão computacional, robótica e GIS (geographic information system). Na computação gráfica, a maioria dos sistemas trabalha apenas com a geometria de pontos e linhas em 3D. Como exemplos de problemas geométricos que surgem no projeto de aplicativos gráfico podemos citar:

• Transformações: Como animar objetos voando ao redor do núcleo de um ciclone? Como você representaria a rotação e a translação dos objetos ao longo do tempo no espaço tridimensional? Como você calcularia a posição exata de um objeto em um determinado momento?
• Interseções geométricas: Dado o mesmo ciclone, como você determinaria se ele atingiu uma casa?
• Orientação: Imagine a visão de uma pessoa dentro de um carro sendo levado pelo ciclone. Como você geraria a cena vista por uma pessoa de dentro do carro?
• Mudança de coordenadas: Imagine que há várias pessoas no carro e a posição de cada uma é conhecida em relação a um sistema de coordenadas centrado no carro. Conhecemos a posição do carro com relação ao mundo. Qual a posição de cada pessoa em relação ao mundo?
• Reflexão e refração: Uma taça cheia de um vinho branco espumante está sobre uma mesa. Uma luz brilhante ilumina o vidro de um lado. A luz passa pelo copo, pelo líquido e por bolhas dentro do líquido e projeta um padrão interessante de regiões claras e escuras na mesa do outro lado do copo. Como você faria para simular esse efeito? A taça é substituída por uma escultura de metal brilhante, e agora, em vez de passar pela taça, a luz é refletida pela complexa superfície da escultura e é lançada sobre a mesa.

Esses exemplos de problemas geométricos são fundamentais para a computação gráfica e, nas próximas aulas, nosso objetivo será apresentar as ferramentas necessárias para responder a essas perguntas. Existem vários sistemas geométricos formais que surgem naturalmente em aplicações de computação gráfica. Os principais são:

• Geometria Afim: A geometria de “coisas planas” simples como pontos, linhas, planos, segmentos de linha, triângulos, etc. Trata-se de um formalismo mais simples que não possui uma definida para propriedades básicas como distância, ângulo ou orientação.
• Geometria Euclidiana: Trata-se do sistema geométrico que nos é mais familiar. Ele aprimora a geometria afim adicionando noções como distâncias, ângulos e orientações (como sentido horário e anti-horário).
• Geometria Projetiva: Na geometria euclidiana, não há noção de infinito, como na aritmética padrão que não permite divisão por zero. No entanto, em CG muitas vezes precisamos lidar com o infinito. Por exemplo, duas linhas paralelas no espaço tridimensional podem se encontrar em um ponto de fuga comum em uma renderização em perspectiva. Pense no ponto onde dois trilhos de trem parecem se encontrar. O cálculo desse ponto de fuga exige que consideremos pontos no infinito. Veremos como a geometria projetiva permite isso.

Além de geometria, vamos fazer uso extenso de álgebra linear para representar, de forma concreta, esses sistemas geométricos abstratos. De forma semelhante como fazemos uso de estruturas concretas como arrays para representar um tipo abstrato de dados como uma pilha. Vamos começar nossa discussão pela geometria afim, por ser a mais simples.

9.1. Geometria Afim

Os elementos básicos da geometria afim são:

• escalares: que podemos considerar como números reais;
• pontos: que definem posições no espaço; e
• vetores livres (ou simplesmente vetores): que possuem direção e magnitude, mas não possuem posição, daí serem chamados de livres, pois flutuam livremente no espaço. Existem um vetor especial chamado de vetor zero (\(\vec{0}\)), que não tem módulo, tal que \(\vec{v} + \vec{0} = \vec{0}+\vec{v} = \vec{v}\).

Observe que na geometria afim não há um ponto zero ou origem do espaço afim. Essa omissão é intencional. Assim, nenhum ponto é especial em relação a outro ponto. Apesar dessa ser uma característica intrínseca do espaço afim, vamos precisar “adotar” uma origem para representar coordenadas no computador.

Observe que vetores e pontos podem ser representados da mesma forma, como uma lista de coordenadas. Mas então, por que fazer uma distinção entre esses elementos? A resposta simples seria: pois são elementos distintos. Na computação muitas vezes usamos tipos abstratos diferentes que compartilham a mesma representação, com por exemplo, pilhas e filas.

Como pontos e vetores são conceitualmente diferentes, não é surpreendente que as operações que podem ser aplicadas a eles sejam diferentes. Por exemplo, faz todo o sentido multiplicar um vetor e um escalar. Geometricamente, isso corresponde a esticar o vetor por essa quantidade. Também faz sentido adicionar dois vetores. Isso envolve a regra usual de juntar o fim de um vetor com o início de outro, como você deve ter visto em cursos de álgebra linear. Não é tão claro, no entanto, o que significa multiplicar um ponto por um escalar, embora faça sentido adicionar um vetor a um ponto, por exemplo, para representar o “deslocamento” de outro ponto.

Usaremos as seguintes convenções para denotar pontos e vetores. Os pontos serão indicados por letras romanas maiúsculas, como \(P\), \(Q\) e \(R\). Os vetores serão indicados com letras minúsculas romanas, como : \(u\), \(v\) e \(w\), e muitas vezes para enfatizar isso, adicionaremos uma seta (por exemplo, \(\vec{u}\), \(\vec{v}\), \(\vec{w}\)). Escalares serão representados como letras gregas minúsculas (por exemplo, \(\alpha\), \(\beta\), \(\gamma\)). Em nossos programas, os escalares serão traduzidos para romano (por exemplo, \(a\), \(b\), \(c\)). No entanto, nem sempre vamos respeitar essas convenções ao longo do texto. Por exemplo, podemos usar \(c\) (letra minúscula) para denotar o ponto central de um círculo ou \(R\) (letra romana) para denotar o raio escalar de um círculo.

9.1.1. Operações afins

A tabela a seguir mostra as combinações válidas entre escalares, pontos e vetores, como você já deve ter visto em cursos de álgebra linear. A Figura Fig. 9.1 ilustra algumas dessas operações.

Table 9.1 Combinações válidas entre escalares, pontos e vetores

Operação	Resultado	Exemplos
multiplicação de vetor por escalar	vetor	\(vetor <= \alpha \cdot vetor\); ou \(vetor <= vetor / \alpha\)
soma de vetores	vetor	\(vetor <= vetor + vetor\); ou \(vetor <= vetor - vetor\)
soma ponto com vetor	ponto	\(ponto <= ponto + vetor\); ou \(ponto <= ponto - vetor\)

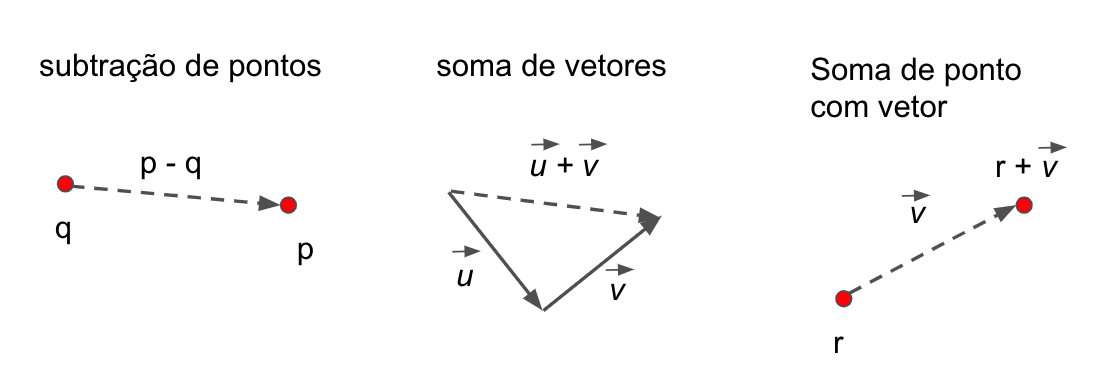
Fig. 9.1 Exemplo de operações válidas com escalares, pontos e vetores.

9.1.2. Combinações afins

Acabamos de ver que a multiplicação de pontos um escalar assim como a soma de pontos não são operações válidas no espaço afim. No entanto, há um tipo de combinação particular que vamos consider válida, chamada de combinação afim de pontos.

Essa combinação surge naturalmente quando desejamos interpolar pontos. Por exemplo, considere dois pontos \(P\) e \(Q\) e o seu ponto médio \(R\), ou ainda, um ponto intermediário qualquer que divide o segmento \(\overline{PQ}\) na proporção \(\alpha\) e \(1-\alpha\), para algum \(alpha \in [0,1]\). Assim, quando \(\alpha=0.5\), o ponto \(R\) estará no meio de \(\overline{PQ}\). Podemos fazer esse calculo usando o vetor \(Q-P\), escalando-o por \(\alpha\) e somando ao ponto \(P\):

\(R = P + \alpha (Q - P)\).

Uma segunda forma de pensar nesse problema é considerar \(R\) como uma média ponderada dos pontos \(P\) e \(Q\). Baseado nessa ideia, poderíamos escrever:

\(R = (1-\alpha) P + \alpha Q\).

Como \(\alpha\) varia entre 0 e 1, o ponto \(R\) varia entre \(P\) e \(Q\). Observe ainda que, para valores negativos de \(\alpha\) podemos obter pontos à esquerda de \(P\) (como ilustrado na Figura Fig. 9.2) e, para valores de \(\alpha\) maiores que 1, obtemos pontos à direita de \(Q\). O caso particular onde \(\alpha \in [0,1]\) é chamado de combinação convexa.

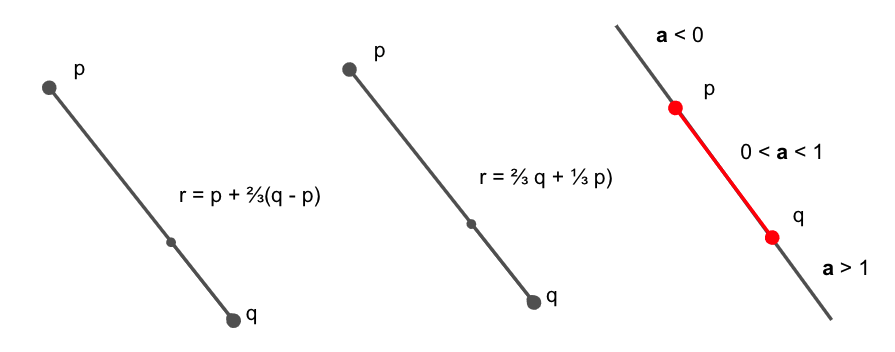
Fig. 9.2 Exemplo de combinações afim de pontos.

Vamos portanto considerar válidas as seguintes operações com pontos no espaço afim:

• Combinação afim: Dada uma sequência de pontos \(P_1, P_2, \ldots , P_n\), uma combinação afim é qualquer soma da forma

  \(\alpha_1 P_1 + \alpha_2 P_2 + \ldots + \alpha_n P_n\),

onde \(\alpha_i\) são escalares tal que \(\sum_i \alpha_i = 1\).

• Combinação convexa: é uma combinação afim que respeita também a restrição de \(\alpha_i \ge 0\) para todo \(1 \le i \le n\).

Combinações afins e convexas têm vários usos interessantes na CG. Por exemplo, quaisquer três pontos não colineares determinam um plano. Existe uma correspondência 1-1 entre os pontos neste plano e as combinações afins desses três pontos. Da mesma forma, há uma correspondência 1-1 entre os pontos no triângulo determinados por esses pontos e as combinações convexas dos pontos. Em particular, o ponto \((1/3)P + (1/3)Q + (1/3)R\) é o baricentro do triângulo. Às vezes vamos abusar um pouco a notação e escreveremos expressões do seguinte tipo (que são claramente ilegais):

\(R = (P + Q) / 2\)

Permitiremos esse tipo de abuso de notação desde que fique claro que representa uma combinação afim legal. Para ver se você entendeu essa notação, considere as seguintes questões (procure pensar antes de ler as respostas):

• Dados três pontos no espaço 3D, qual é a união de todas as suas combinações afins?

  • Resposta: o plano contendo os 3 pontos.

• Qual é a união de todas as suas combinações convexas?

  • Resposta: O triângulo definido pelos três pontos e seu interior.

9.2. Geometria Euclidiana

A geometria afim não possui ferramentas para tratar de ângulos e distâncias. A geometria euclidiana é uma extensão da geometria afim que inclui o operador produto interno. Assim, por ser uma extensão, tudo que vale para o espaço afim valerá também para o espaço euclidiano.

O produto interno é um operador que mapeia dois vetores para um escalar. O produto de \(\vec{u}\) e \(\vec{v}\) será denotado por \((\vec{u},\vec{v})\).

9.2.1. Propriedades do produto interno

• Positividade: \((\vec{u},\vec{u}) \ge 0\) e \((\vec{u},\vec{u}) = 0\) se e somente se \(\vec{u}=0\).
• Simetria: \((\vec{u},\vec{v}) = (\vec{v},\vec{u})\).
• Bilinearidade: \((\vec{u},\vec{v}+\vec{w})\) = \((\vec{u},\vec{v})\) + \((\vec{u},\vec{w})\) e \((\vec{u}, \alpha \vec{v}) = \alpha (\vec{u},\vec{v})\).

O produto escalar é um caso especial do produto interno usado comumente na geometria euclidiana. Vamos denotar o produto escalar de \(\vec{u}\) e \(\vec{v}\) por \(\vec{u} \cdot \vec{v}\). Note que o produto interno (e escalar) são definidos apenas para vetores (e não para pontos).

Usando o produto escalar podemos agora definir vários conceitos que não estavam definidos no espaço afim, como ilustrado na Figura Fig. 9.3.

• Comprimento: de um vetor \(\vec{v}\) é definido por \(\lVert\vec{v}\rVert = \sqrt{\vec{v} \cdot \vec{v}}\)

• Normalização: de um vetor \(\vec{v}\) não nulo é um vetor de mesma direção mas de comprimento unitário, que pode ser calculado como \(\vec{v}/\lVert\vec{v}\rVert\). Vamos denotar por \(\hat{v}\).

• Distância: entre dois pontos \(dist(P, Q) = \lVert P-Q \rVert\)

• Ângulo: entre dois vetores não nulos \(\vec{u}\) e \(\vec{v}\) é

  \(ang(\vec{u}, \vec{v}) = \mbox{cos}^{-1} ( \vec{u} \cdot \vec{v} / \lVert \vec{u} \rVert \lVert \vec{v} \rVert) = \mbox{cos}^{-1} (\hat{u} \cdot \hat{v})\).

Você pode deduzir essa equação aplicando a lei dos cossenos, resultando em um ângulo no intervalo \([0, \pi]\). Observe que isso não nos fornece um ângulo com sinal e, por isso, não podemos dizer a orientação de \(\vec{u}\) com relação a \(\vec{v}\), por exemplo, se \(\vec{u}\) está no sentido horário ou anti-horário em relação a \(\vec{v}\). Discutiremos ângulos com sinal quando considerarmos o produto vetorial.

• Ortogonalidade: os vetores \(\vec{u}\) e \(\vec{v}\) são ortogonais (ou perpendiculares) se \(\vec{u} \cdot \vec{v} = 0\)

• Projeção ortogonal: dado um vetor \(\vec{u}\) e um vetor não nulo \(\vec{v}\), muitas vezes é conveniente decompor \(\vec{u}\) na soma de dois vetores \(\vec{u} = \vec{u_1} + \vec{u_2}\), tal que \(\vec{u_1}\) seja paralelo a \(\vec{v}\) e \(\vec{u_2}\) seja ortogonal a \(\vec{v}\).

  \(\vec{u_1} = \frac{\vec{u} \cdot \vec{v}}{\vec{v} \cdot \vec{v}} \vec{v}\), \(\vec{u_2} = \vec{u}-\vec{u_1}\)

Note que, caso \(\vec{v}\) seja um vetor unitário (de comprimento 1), não é necessário calcular o denominador de \(\vec{u_1}\). Esse vetor \(\vec{u_1}\) é chamado de projeção ortogonal de \(\vec{u}\) em \(\vec{v}\).

Fig. 9.3 Propriedades do produto escalar.

9.3. Onde estamos e para onde vamos?

Interrompemos por um momento a programação com WebGL para recordar alguns fundamentos de geometria e álgebra linear relacionados à geometria afim e euclidiana, como os conceitos de ponto e vetor, operações com escalares, pontos e vetores, e o operador produto escalar que usamos para calcular ângulos e distâncias.

Na próxima aula continuaremos a recordação de outros fundamentos, como frame de coordenadas, coordenadas homogêneas e o operador de produto vetorial.

9.4. Exercícios

1. Implemente a função (classe) Ponto2D em JavaScript. Sua classe deve incluir os atributos que achar convenientes e ao menos os métodos:

   • sub: que retorna um vetor resultante da subtração do ponto com outro ponto.
   • mix: que retorna um ponto resultante da mistura do ponto com outro na proporção \(alpha\).

2. Implemente a função (classe) Vetor2D em JavaScript. Sua classe deve incluir os atributos que achar convenientes e ao menos os métodos:

   • mult: que retorna o vetor multiplicado por um escalar \(\alpha\)
   • add: que retorna o vetor resultante da soma do vetor com outro vetor.

3. Dados os vetores \(\vec{u} = (3, 4)\) e \(\vec{v} = (5, 2)\), calcule os vetores \(\vec{u_1}\) e \(\vec{u_2}\) que formam a projeção ortogonal de \(\vec{u}\) em \(\vec{v}\). Verifique que \(\vec{u} = \vec{u_1} + \vec{u_2}\) e que \(\vec{u_2}\) é perpendicular a \(\vec{v}\).

9.5. Para saber mais

• Aula 5 das notas de aula do Prof. Dave Mount
• Produto escalar na Wikipédia.
• Capítulo 4 do livro “Interactive Computer Graphics, 8th edition” de Angel e Shreiner.
• Capítulo 5 do livro “Computer Graphics - principles and practice”, Foley et al.

Outra boa fonte de informação sobre como resolver problemas geométricos computacionalmente é a série de livros intitulada “Graphics Gems”. Cada livro é uma coleção de muitos problemas gráficos simples e fornece algoritmos para resolvê-los.