Problema de revisão 1 (sobre listas)

Dada uma sequência \(x_1, x_2, ..., x_n\) de \(n\) números inteiros, verifique se existem dois segmentos consecutivos iguais nesta seqüência, isto é, se existem \(i\) e \(m\) tais que:

\[x_i, x_{i+1}, ... , x_{i+m-1} = x_{i+m}, x_{i+m+1}, ... , x_{i+2m-1}\]

Imprima, caso existam, os valores de \(i\) e \(m\).

Exemplo: Na seqüência 7, 9, 5, 4, 5, 4, 8, 6 existem i=3 e m=2.

In [1]:

n = int(input("Digite o número de elementos na sequência: "))

sequencia = []
for i in range(1,n+1):
    sequencia.append(int(input("Digite o %do. número da sequência: " %i)))
    
i = 0
achou_seg = False
while i < n and not achou_seg:
    # procura o valor da posição i da sequencia em outra posição mais adiante
    j = i
    while j < n-1 and not achou_seg:
         j += 1
         if sequencia[i] == sequencia[j]:    
         # achou o valor mais adiante, então verifica os segmentos
            m = j-i
            k = 1
            while k < m and j+k < n and sequencia[i+k] == sequencia[j+k]:
                k = k+1
                
            achou_seg = k == m
        
    i += 1

if achou_seg:
    print("Achei segmentos consecutivos iguais: i = %d e m = %d" %(i,m))
else:
    print("Não achei segmentos consecutivos iguais")

Digite o número de elementos na sequência: 8
Digite o 1o. número da sequência: 7
Digite o 2o. número da sequência: 9
Digite o 3o. número da sequência: 5
Digite o 4o. número da sequência: 4
Digite o 5o. número da sequência: 5
Digite o 6o. número da sequência: 4
Digite o 7o. número da sequência: 8
Digite o 8o. número da sequência: 6
Achei segmentos consecutivos iguais: i = 3 e m = 2

Problema de revisão 2 (sobre listas e matrizes)

Faça uma função que recebe como parâmetro um número inteiro n e imprime as n primeiras linhas do triângulo de Pascal.

Por exemplo, para n = 6, sua função deve imprimir:

1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1

É possível implementar a função usando apenas uma lista?

Solução 1: usando matrizes

In [2]:

def imprime_triangulo(n):
    # Cria a matriz inicialmente com valores
    # Para facilitar os calculos, incluiremos na matriz uma 
    # coluna adicional, que servirá como "borda" à esquerda
    matriz = []
    for i in range(n):
        matriz.append([0] * (n+1))
    
    # Calcula os números do triângulo de Pascal
    matriz[0][1] = 1
    for i in range(1,n):
        for j in range(1,i+2):
            matriz[i][j] = matriz[i-1][j-1] + matriz[i-1][j]
    
    # Imprime os números do triângulo
    for i in range(n):
        for j in range(1,i+2):
            print("%4d" %matriz[i][j], end="  ")
        print()

# Testa a função
imprime_triangulo(6)

   1  
   1     1  
   1     2     1  
   1     3     3     1  
   1     4     6     4     1  
   1     5    10    10     5     1

Solução 2: usando somente uma lista

In [3]:

def imprime_triangulo(n):
    # Cria lista com n+1 posições valendo 0
    linha = [0] * (n+1)
    
    # Calcula e imprime os números do triângulo de Pascal
    linha[1] = 1
    print("%4d" %1)
    for i in range(1,n):
        for j in range(i+1,0,-1):
            linha[j] = linha[j-1] + linha[j]
    
        for j in range(1,i+2):
            print("%4d" %linha[j], end="  ")
        print()

# Testa a função
imprime_triangulo(6)

   1
   1     1  
   1     2     1  
   1     3     3     1  
   1     4     6     4     1  
   1     5    10    10     5     1

Problema de revisão 3 (sobre strings e caracteres)

Em criptografia, a Cifra de César, também conhecida como cifra de troca, código de César ou troca de César, é uma das mais simples e conhecidas técnicas de criptografia. É um tipo de cifra de substituição na qual cada letra do texto é substituída por outra, que se apresenta no alfabeto abaixo dela um número fixo de vezes.

Por exemplo, com uma troca de três posições, A seria substituído por D, B se tornaria E, e assim por diante. O nome do método é em homenagem a Júlio César, que o usou para se comunicar com os seus generais.

Aqui está uma cifra de César usando uma rotação à esquerda de três posições (o parâmetro de troca, três neste caso, é usado como chave):

Normal: a vEloz raposa MARROM saLTou sobre O cachorro CAnsado

Cifrado: d yHorc udsrvd PDUURP vdOWrx vreuh R fdfkruur FDqvdgr

Faça uma função que receba como parâmetro uma frase e um inteiro positivo k e devolva a codificação da frase pela cifra de César com k como chave. Considere apenas os caracteres ASCII (ou seja, caracteres sem acentuação).

In [4]:

def encripta(frase, k):
    '''
        (str, int) -> str
        Função que recebe como entrada uma frase e uma chave k,
        e devolve a codificação da frase segundo a Cifra de César,
        usando k como chave
    '''
    
    ordA = ord('A')
    orda = ord('a')
    cifra = ""
    for c in frase:
        if "A" <= c <= "Z": 
            # o caracter é uma letra maiúscula
            cifra += chr(ordA + ((ord(c) - ordA + k) % 26)) 
        elif "a" <= c <= "z":
            # o caracter é uma letra minúscula
            cifra += chr(orda + ((ord(c) - orda + k) % 26)) 
        else:
            cifra += c
            
    return cifra

# Teste da função

frase = "a vEloz raposa MARROM saLTou sobre O cachorro CAnsado"
cifra = encripta(frase,3)
print("Frase original:  ", frase)
print("Frase encriptada:", cifra)

Frase original:   a vEloz raposa MARROM saLTou sobre O cachorro CAnsado
Frase encriptada: d yHorc udsrvd PDUURP vdOWrx vreuh R fdfkruur FDqvdgr

Problema de revisão 4 (sobre funções e reais)

Obs.: Este problema corresponde ao exercício 4 da lista de exercícios sobre Funções - Parte 1.

Faça uma função arctan que recebe um número real x \(\in [0,1]\) e devolve uma aproximação do arco tangente de x (em radianos) através da série

\[ arctan(x) = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + ... \]

incluindo todos os termos da série até \(|\frac{x^k}{k}| < 0,0001\).

In [5]:

def arctan(x):
    '''
        (float) -> float
        Função que recebe um número real x, tal que 0 <= x <= 1,
        e devolve uma aproximação do arco tangente de x em
        radianos.
    '''
    eps = 0.0001
    soma = termo = pot = x
    k = 1
    while termo >= eps or -termo >= eps: 
        k += 2
        pot *= -x*x 
        termo = pot/k
        soma = soma + termo
        
    return soma

Faça uma função angulo que recebe um ponto de coordenadas cartesianas reais (x,y), com x > 0 e y > 0 e devolve o ângulo formado pelo vetor (x,y) e o eixo horizontal.

Exemplos: Observe a figura abaixo e os ângulos (aproximadas) correspondentes aos pontos marcados.

Ponto	Ângulo
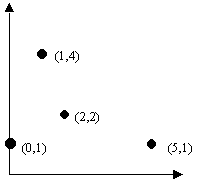
(0,1)	90 graus
(2,2)	45 graus
(1,4)	75 graus
(5,1)	11 graus

Use a função criada no item (a) no cálculo do ângulo. Note que a função só calcula o arco tangente de números entre 0 e 1, e o valor devolvido é o ângulo em radianos (use o valor \(\pi\) = 3.14 radianos = 180 graus).

Para calcular o valor do ângulo \(\alpha\) pedido, use a seguinte fórmula:

\[\alpha = \begin{cases} arctan(\frac{y}{x}), & \mbox{caso }y<x \\ \frac{\pi}{2} - arctan(\frac{x}{y}), & \mbox{no caso contrário}\end{cases}\]

In [6]:

PI = 3.14   

# Função extra
def graus(x):
    '''
        (float) -> float
        Função que recebe um valor em radianos e
        devolve o valor correspondente em graus.
    '''
    return 180*x/PI

def angulo(x,y):
    '''
        (float,float) -> float
        Função que recebe como entrada um ponto (x,y) e 
        devolve o ângulo em graus que o vetor (x,y) forma
        com o eixo horizontal.
    '''
    if x == 0 and y == 0:
        return -1       # Para (0,0), não há ângulo!
    
    if y < x:
        ang = arctan(y/x)
    else:
        ang = PI/2 - arctan(x/y)
        
    return graus(ang)

Faça um programa que, dados n pontos do primeiro quadrante (x >= 0 e y >= 0) através de suas coordenadas cartesianas, determina o ponto que forma o menor ângulo com o eixo horizontal. Use a função do item anterior.

In []:

def main():

    n = int(input("Digite quantidade de pontos: "))
    angmin = 100   # qualquer valor acima de 90 vale como inicialização
  
    for i in range(1,n+1):
        x = float(input("Digite a coordenada x do %do. ponto: " %i))
        y = float(input("Digite a coordenada y do %do. ponto: " %i))
    
        ang = angulo(x,y)
        if ang == -1:
            print("Ponto na origem, será desconsiderado")
        elif ang < angmin:
            angmin = ang;
            xmin = x
            ymin = y
      
    print("Ponto de menor ângulo: (%f,%f)" %(xmin,ymin))
    print("Menor ângulo: %f graus" %angmin)

# Executa o programa principal
main()

Problema de revisão 5 (sobre listas)

Escreva uma função que recebe como parâmetro uma lista de números reais e uma posição k dessa lista, e devolve o índice do elemento mínimo entre X[k], X[k+1], ..., X[n], sendo n o tamanho da lista.
Usando a função do item anterior, crie uma função que recebe como parâmetro uma lista de números reais e a ordene. A sua função não deve devolver nenhuma valor; portanto, ela deve alterar a própria lista passada como parâmetro.

In []:

def posicao_minimo(lista, k):
    pos_min = k
    while k < len(lista) - 1:
        k += 1
        if lista[k] < lista[pos_min]:
            pos_min = k
            
    return pos_min

def ordena(lista):
    for i in range(len(lista)):
        j = posicao_minimo(lista,i)
        aux =  lista[i]
        lista[i] = lista[j]
        lista[j] = aux

# Testa a função ordena
lista = [9.8, 3.567, 2.782, 12.6379, 1.384, 0.2541, 7.29]
print("Lista não ordenada:", lista)
ordena(lista)
print("Lista ordenada    :", lista)

MAC2166 - Introdução à Computação¶

20/05/2014 - Aula 15¶

Exercícios de Revisão para a Prova 2