Linguagem C - Problema 9
Dada uma matriz real \(A_{m \times n}\), verificar se existem elementos repetidos em \(A\).
Obs.: Esse problema é o exercício 4 da lista de exercícios sobre matrizes.
#### Solução
Linguagem C - Problema 10
Um sistema de equações lineares com \(nl\) equações pode ser representado por uma matriz \(A_{nl \times nc}\), onde cada equação tem \(nc\) coeficientes.
Um vetor real \(X\) com \(nc\) elementos é apresentado como resultado de um sistema de equações lineares \(A X = B\), onde \(B\) é um vetor real com \(nl\) elementos.
Escreva um programa que leia \(A\), \(X\) e \(B\), e calcula e imprime o erro quadrático médio da solução \(X\), dado por \(\sum_i{(((AX)[i] - B[i])^2) / nl}\).
Para resolver esse problema, implemente e utilize as seguintes funções:
- Escreva uma função com protótipo:
void le_vetor(float V[MAX], int nc);
que lê \(nc\) reais e carrega em \(V\).
Solução
- Escreva uma função com protótipo:
void le_matriz(float M[MAX][MAX], int nl, int nc);
que lê \(nl x nc\) reais e carrega em \(M\).
Pode ser interessante utilizar a função do item (a).
Solução
- Escreva uma função com protótipo:
void mult(float A[MAX][MAX], float X[MAX], float Y[MAX], int nl, int nc);
que recebe uma matriz real \(A_{nl \times nc}\) e um vetor real \(X\) com \(nc\) elementos, e devolve em \(Y\) o produto \(A \times X\).
Solução
Dizemos que uma matriz quadrada inteira é um quadrado mágico se a soma dos elementos de cada linha, a soma dos elementos de cada coluna e a soma dos elementos das diagonais principal e secundária são todas iguais.
Exemplo: A matriz
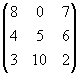
é um quadrado mágico.
Dada uma matriz quadrada \(A_{n \times n}\) , verificar se \(A\) é um quadrado mágico.
Obs.: Esse problema é o exercício 7 da lista de exercícios sobre matrizes.
#### Solução
Dizemos que uma matriz \(A_{n \times n}\) é um quadrado latino de ordem \(n\) se em cada linha e em cada coluna aparecem todos os inteiros \(1,2,3,\ldots,n\) (ou seja, cada linha e coluna é permutação dos inteiros \(1,2,\ldots,n\)).
Escreva uma função que recebe como parâmetros um inteiro \(n\), um vetor \(V\) com \(n\) inteiros e verifica se em \(V\) ocorrem todos os inteiros de \(1\) a \(n\).
Usando a função acima, verifique se uma dada matriz inteira \(A_{n \times n}\) é um quadrado latino de ordem \(n\).
Solução