MAC2166 - Introdução à Computação¶
01/06/2017 - Aula 17 - Recursão¶
A definição a seguir encontra-se na Tradução do livro “How to Think Like a Computer Scientist: Interactive Version”, de Brad Miller e David Ranum:
- Recursão é um método de resolução de problemas que envolve quebrar um problema em subproblemas menores e menores até chegar a um problema pequeno o suficiente para que ele possa ser resolvido trivialmente.
- Normalmente recursão envolve uma função que chama a si mesma.
- Embora possa não parecer muito, a recursão nos permite escrever soluções elegantes para problemas que, de outra forma, podem ser muito difíceis de programar.
Problema 17.1
Escreva um função que calcule o fatorial de um número.
Solução 1 (sem recursiva)
Calcula um produtório: $fatorial(n) = \Pi_{i = 1}^{n} i$
def fatorial(n):
''' (int) -> int
Função que recebe um número natural n e devolve n!
'''
fat = 1
i = 1
while i <= n:
fat *= i
i += 1
return fat
def main():
n = int(input("Digite o número do qual se deseja calcular o fatorial: "))
print("A fatorial de %d é %d." %(n, fatorial(n)))
######################
main()
Solução 2 (com recursão)
Calcula a seguinte recorrência: $fatorial(n) = \left\{\begin{matrix} 1 & \text{, se }n = 0\\ n * fatorial(n-1) & \text{, se }n > 0 \end{matrix}\right.$
def fatorial(n):
''' (int) -> int
Função que recebe um número natural n e devolve n!
'''
if n == 0: # Caso base
return 1 # Solução direta
else:
return n * fatorial(n-1) # Chamada recursiva
def main():
n = int(input("Digite o número do qual se deseja calcular o fatorial: "))
print("A fatorial de %d é %d." %(n, fatorial(n)))
######################
main()
Problema 17.2
Escreva uma função que calcula o valor de um número real x elevado a um número natural n.
Solução 1 (sem recursão)
Calcula um produtório: $potencia(x,n) = \Pi_{i=1}^{n} x $
def potencia(x, n):
pot = 1.0
while n > 0:
pot *= x
n -= 1
return pot
def main():
base = float(input("Digite o número real da base: "))
expoente = int(input("Digite o número natural do expoente: "))
print("O valor de %f elevado a %d é: %f." %(base, expoente, potencia(base,expoente)))
######################
main()
Solução 2 (com recursão)
Calcula a seguinte recorrência: $potencia(x,n) = \left\{\begin{matrix} 1 & \text{, se }n = 0\\ x * potencia(x,n-1) & \text{, se }n > 0 \end{matrix}\right.$
def potencia(x, n):
if n == 0: # Caso base
return 1.0 # Solução direta
else:
return x * potencia(x, n-1) # Chamada recursiva
def main():
base = float(input("Digite o número real da base: "))
expoente = int(input("Digite o número natural do expoente: "))
print("O valor de %f elevado a %d é: %f." %(base, expoente, potencia(base,expoente)))
######################
main()
Solução 3 (outra com recursão)
Calcula a seguinte recorrência:
$potencia(x,n) = \left\{\begin{matrix} 1 & \text{, se }n = 0\\ potencia(x,n//2)^2 = potencia(x,n//2) * potencia(x,n//2) & \text{, se }n > 0\text{ e } n\text{ é par}\\ x * potencia(x,n//2)^2 = x * potencia(x,n/2) * potencia(x,n/2) & \text{, se }n > 0\text{ e } n\text{ é ímpar} \end{matrix}\right.$
def potencia(x, n):
if n == 0: # Caso base
return 1.0
elif n%2 == 0: # Se n é par...
pot = potencia(x, n//2)
return pot * pot
else: # Se n é ímpar...
pot = potencia(x, n//2)
return pot * pot * x
def main():
base = float(input("Digite o número real da base: "))
expoente = int(input("Digite o número natural do expoente: "))
print("O valor de %f elevado a %d é: %f." %(base, expoente, potencia(base,expoente)))
######################
main()
Problema 17.3
Escreva uma função que encontra o maior valor de uma lista de números inteiros que contém ao menos um número.
Solução 1 (sem recursão)
def main():
print("Iniciando leitura da lista: ")
lista = le_lista()
maior = lista[0]
for i in range(1,len(lista)):
if lista[i] > maior:
maior = lista[i]
print("O maior valor encontrado na lista é:", maior)
######################
def le_lista():
'''(None) -> list
Le do teclado uma sequencia de numeros inteiros e retorna
uma lista com os elementos lidos.
'''
seq = []
n = int(input("Digite o tamanho da lista:"))
for i in range(n):
# le o proximo numero da sequencia
num = int(input("Digite o %do. numero da lista: " %(i+1)))
seq.append(num)
return seq
######################
main()
Solução 2 (com recursão)
def main():
print("Iniciando leitura da lista: ")
lista = le_lista()
print("O maior valor encontrado na lista é:", maior(lista))
######################
def le_lista():
'''(None) -> list
Le do teclado uma sequencia de numeros inteiros e retorna
uma lista com os elementos lidos.
'''
seq = []
n = int(input("Digite o tamanho da lista:"))
for i in range(n):
# le o proximo numero da sequencia
num = int(input("Digite o %do. numero da lista: " %(i+1)))
seq.append(num)
return seq
######################
def encontra_maior(L, n):
''' (list, int) -> int
Devolve o maior valor entre os valores {L[0], L[1], ..., L[n-1]},
onde n é o numero de elementos da lista de inteiros L.
'''
if n == 1: # Caso trivial: só há um valor possível
return L[0]
else:
m = encontra_maior(L, n-1)
# devolve o menor valor entre os dois seguintes: L[n-1] e o menor em {L[0], L[1], ..., L[n-2]}
if m > L[n-1]:
return m
else:
return L[n-1]
def maior(L):
''' (list) -> int
Devolve o maior valor existente na lista de inteiros L.
'''
return encontra_maior(L, len(L))
######################
main()
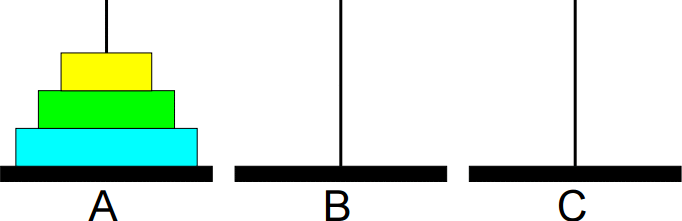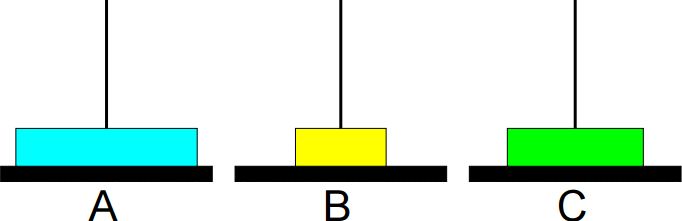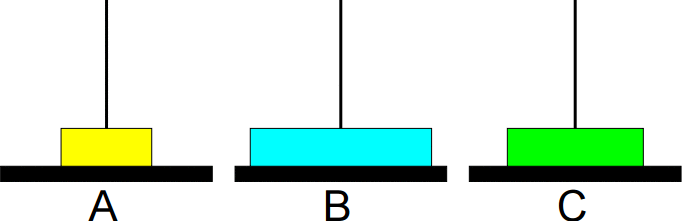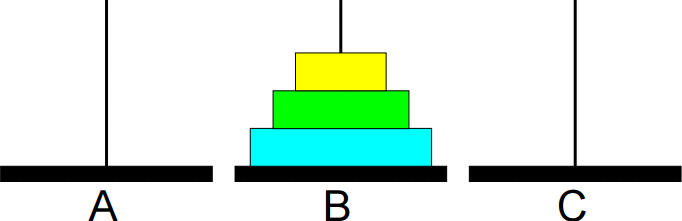
Torre de Hanói
Segunda a Wikipédia, "A Torre de Hanói é um "quebra-cabeça" que consiste em uma base contendo três pinos, em um dos quais são dispostos alguns discos uns sobre os outros, em ordem crescente de diâmetro, de cima para baixo. O problema consiste em passar todos os discos de um pino para outro qualquer, usando um dos pinos como auxiliar, de maneira que um disco maior nunca fique em cima de outro menor em nenhuma situação."
Exemplo
As imagens a seguir (criadas pelo prof. Paulo Miranda, do DCC-IME-USP) ilustram como resolver uma torre de Hanói com 3 discos:
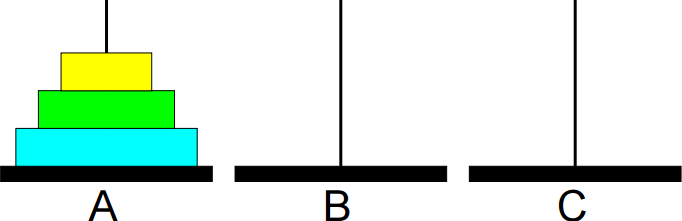
1º passo: Mover de A para B.
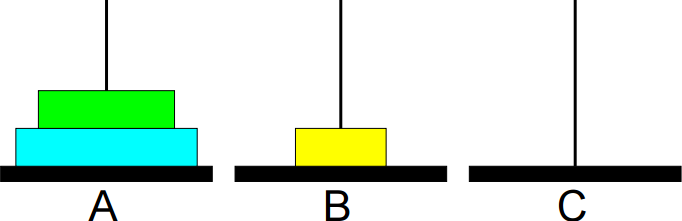
2º passo: Mover de A para C.
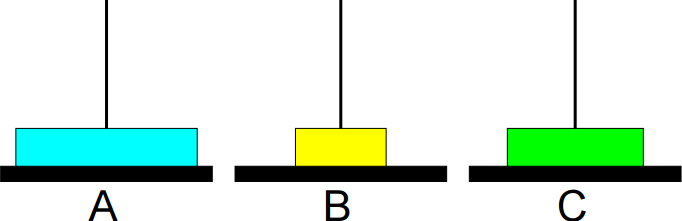
3º passo: Mover de B para C.
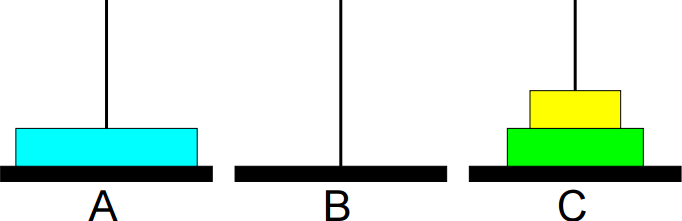
4º passo: Mover de A para B.
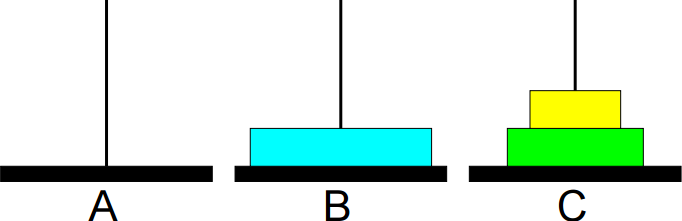
5º passo: Mover de C para A.
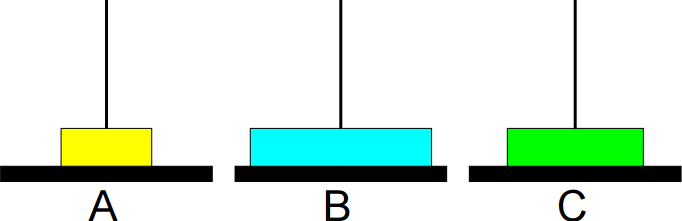
6º passo: Mover de C para B.
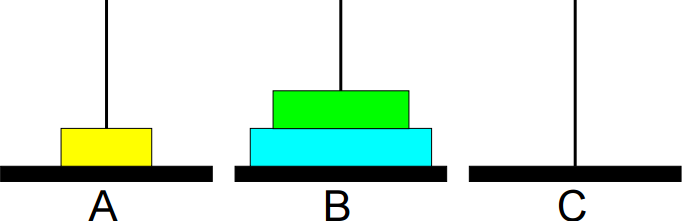
7º passo: Mover de A para B.
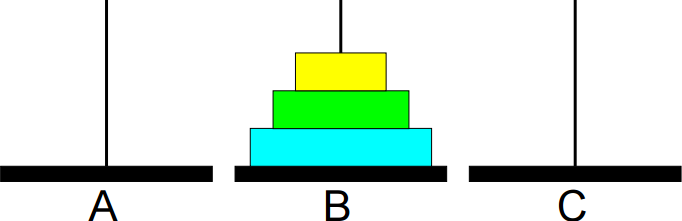
Animação da sequência completa de movimentos:
A imagem animada abaixo (da Wikipédia) ilustra a solução de uma torre com 4 pinos:

O número de movimentos necessários para mover $n$ discos do pino A para o pino B é $2^n - 1$.
Problema 17.4
Escreva um programa que, dado um número n representando a quantidade de discos de diâmetros diferentes em uma torre de Hanói, imprima os passos necessários para transferir os discos do pino A para o pino B da torre, usando o pino C como auxiliar, nunca colocando discos maiores sobre menores.
Solução
def hanoi(n, orig, dest, aux):
if n == 1:
print("Mover de",orig,"para",dest)
else:
hanoi(n-1, orig, aux, dest)
print("Mover de",orig,"para",dest)
hanoi(n-1, aux, dest, orig)
######################
def main():
n = int(input("Digite a quantidade de discos da torre: "))
hanoi(n, "A", "B", "C")
######################
main()
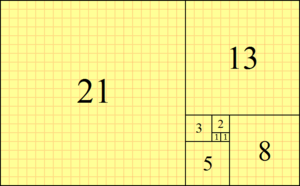
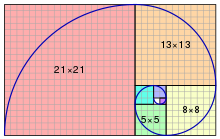
A Sequência de Fibonacci
Segundo a Wikipédia, a Sequência de Fibonacci é "uma sequência de números inteiros, começando normalmente por 0 e 1, na qual, cada termo subsequente corresponde a soma dos dois anteriores. A sequência recebeu o nome do matemático italiano Leonardo de Pisa, mais conhecido por Fibonacci, que descreveu, no ano de 1202, o crescimento de uma população de coelhos, a partir desta. Tal sequência já era no entanto, conhecida na antiguidade."
Portanto, começando por 1, os números que compõem a sequência de Fibonacci são:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, ...
A sequência é definida recursivamente pela fórmula abaixo:
$F_n = F_{n-1} + F_{n-2}$
$F_1 = 1\text{, }F_2 = 1 $
A sequência de Fibonacci ocorre com bastante frequência na natureza, no padrão de formação de flores, caracóis...



Problema 17.5
Escreva uma função que recebe um número natural n >= 1 e que devolve o n-ésimo número da sequência de Fibonacci. Obs.: Neste exercício, considere que a sequência de Fibonacci começa com 1 (ou seja, a sequência é: 1, 1, 2, 3, 5, 8, ...).
Solução 1 (sem recursão)
def fibonacci(n):
termo1 = 0
novo_termo = termo2 = 1
for k in range(2,n+1):
novo_termo = termo1 + termo2
termo1 = termo2
termo2 = novo_termo
return novo_termo
######################
def main():
n = int(input("Digite o número do termo da sequência de Fibonacci desejado: "))
print("O %dº termo da sequência de Fibonacci é: %d" %(n,fibonacci(n)))
######################
main()
Solução 2 (com recursão)
def fibonacci(n):
if n <= 1:
return n
else:
return fibonacci(n-1) + fibonacci(n-2)
######################
def main():
n = int(input("Digite o número do termo da sequência de Fibonacci desejado: "))
print("O %dº termo da sequência de Fibonacci é: %d" %(n,fibonacci(n)))
######################
main()