MAC2166 - Introdução à Computação¶
29/06/2017 - Aula 25 - Revisão para a P3¶
Problema 25.1 (Recursão)
Escreva uma função que implemente o algoritmo da Busca Binária (ensinado na aula 18), mas desta vez sua função deve ser recursiva. A função deve receber como parâmetro uma lista ordenada e um número real x e devolver a posição em que x ocorre na lista ou None caso x não esteja na lista.
def busca_binaria_rec(seq, inicio, fim, x):
''' (list, float) -> bool
retorna a posição em que x ocorre na lista ordenada entre as posições
inicio e fim, ou None caso x não esteja entre essas posições,
usando o algoritmo de busca binária.
'''
if inicio > fim:
return None
meio = (inicio + fim) // 2
if x == seq[meio]: # achou x na posição meio
return meio
if x < seq[meio]: # x pode estar na primeira metade da sequência
return busca_binaria_rec(seq, inicio, meio-1, x)
# x pode estar na segunda metade da sequência
return busca_binaria_rec(seq, meio+1, fim, x)
def busca_binaria(seq, x):
return busca_binaria_rec(seq, 0, len(seq)-1, x)
##########################################
# Alguns testes da função busca_binaria
seq = [4, 10, 80, 91, 99, 100, 101]
testes = [80, 50]
print("A sequência usada para testes é: ", seq)
for t in testes:
pos = busca_binaria(seq, t)
if pos is None:
print("Nao achei", t)
else:
print("Achei %d na posição %d" %(t, pos))
Problema 25.2 (Recursão)
Recursão mútua ocorre quando duas(ou mais) funções são definidas uma(s) em termo da(s) outra(s).
Escreva uma função que recebe um número natural maior que zero e devolve True quando o número é par e False no caso contrário. Escreva também uma função que recebe um número natural maior que zero e devolve True quando o número é ímpar e False no caso contrário. As duas funções devem ser mutuamente recursivas.
def é_par(n):
if n == 0: # Caso base da recursão
return True
else:
return é_ímpar(n - 1) # Chamada recursiva (recursão mútua)
def é_ímpar(n):
if n == 0: # Caso base da recursão
return False
else:
return é_par(n - 1) # Chamada recursiva (recursão mútua)
#########################
# Testando as funções
print("10 é par?", é_par(10))
print("10 é ímpar?", é_ímpar(10))
print("11 é par?", é_par(11))
print("11 é ímpar?", é_ímpar(11))
Problema 25.3 (Séries com Números Reais)
Dados $x$ real e $epsilon$ real, $epsilon > 0$, calcular uma aproximação para $sen(x)$ através da seguinte série infinita:
$$ sen(x) = \frac{x}{1!} − \frac{x^3}{3!} + \frac{x^5}{5!} + ... + (−1)^k \frac{x^{2k+1}}{(2k+1)!} +... $$
incluindo todos os termos até que $|\frac{x^{2k+1}}{(2k+1)!}| < epsilon $.
Compare com os resultados de sua calculadora!
import math
def seno(x,eps):
'''
(float) -> float
Função que recebe um número real x e devolve uma
aproximação do seno de x em radianos.
'''
soma = termo = x
k = 1
while termo >= eps or -termo >= eps: # precisamos verificar o valor absoluto do termo,
# porque aqui o termo já tem o sinal nele
k += 2
termo *= -x*x / (k * (k-1))
soma = soma + termo
return soma
######################
# Testa a função seno()
eps = 0.000001
x = math.pi / 2
print("O seno de %f é aproximadamente %f radianos." %(x, seno(x,eps)))
Problema 25.4 (Dicionários)
Escreva um programa que leia um arquivo texto contendo informações sobre preços de produtos em diferentes datas e que mostre como resultado o menor preço que cada produto já teve.
Exemplo: para o arquivo texto precos_produtos.txt que contém as linhas abaixo,
29/06/2017 cebola 2.19
29/06/2017 batata 1.98
29/06/2017 alface 1.88
22/06/2017 beterraba 2.48
22/06/2017 alface 2.00
22/06/2017 cebola 2.03
15/06/2017 beterraba 2.44
15/06/2017 alface 1.75
15/06/2017 batata 2.11
o programa deve mostrar uma listagem como a seguir (a ordem dos produtos na saída pode ser diferente):
Produto: cebola Menor Preço: 2.03
Produto: batata Menor Preço: 1.98
Produto: alface Menor Preço: 1.75
Produto: beterraba Menor Preço: 2.44
def main():
nome_arquivo = input("Digite o nome do arquivo com os preços dos produtos: ")
arquivo = open(nome_arquivo, "r") # abre o arquivo para leitura
menores_precos = {} # cria um dicionário para armazenar pares do tipo (produto:preço),
# que associa um produto ao menor preço encontrado para ele no arquivo
for linha in arquivo:
dados = linha.split() # cria uma lista de strings com os valores separados por espaços na linha
produto = dados[1]
preco = float(dados[2])
if produto not in menores_precos: # verifica se o produto lido da linha atual já está no dicionário
# produto não está no dicionário (é a primeira ocorrência dele no arquivo),
# então ele é colocado no dicionário
menores_precos[produto] = preco
else:
# produto já está no dicionário, então se o novo preço lido para ele
# é menor que o menor preço já encontrado para ele no arquivo anteriormente,
# o novo preço passa a ser o menor e é atualizado no dicionário
if menores_precos[produto] > preco:
menores_precos[produto] = preco
arquivo.close() # fecha o arquivo, pois a leitura dele já terminou
# Percorre as chaves (produtos) do dicionário,
# para mostrar os valores (menores preços) correspondentes
for produto in menores_precos:
print("Produto: %s\t\tMenor Preço: %.2f" %(produto, menores_precos[produto]))
main()
Problema 25.5 (Recursão)
Escreva uma função recursa que implemente o algoritmo de Ordenação por Intercalação (Merge Sort), descrito a seguir.
Merge Sort
Se o tamanho da lista a ser ordenada é maior que 1, então
1.1 divida a lista no meio
1.2 ordene a primeira metade da lista recursivamente
1.3 ordene a segunda metade da lista recursivamente
1.4 intercale as duas metades, criando uma só lista ordenada
1.5 devolva a lista ordenada
Senão, devolva a lista da forma como está (pois uma lista com zero ou mais elementos já está naturalmente ordenada)
A figura animada abaixo, da página do MergeSort na Wikipédia ilustra o funcionamento do algoritmo:
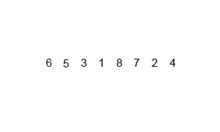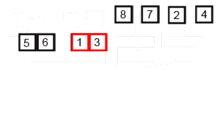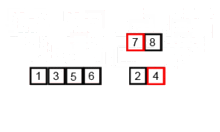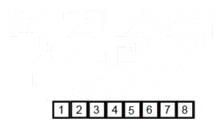
def mergesort(lista):
''' (list) -> None
A função rearranja a lista em ordem crescente.
Ela implementa uma ordenação por intercalação.
'''
print("Dividindo: ",lista) # imprime a lista apenas para auxiliar o entendimento da função
if len(lista) > 1: # Se a lista tem 2 ou mais elementos,
# então ela precisa ser ordenada
meio = len(lista)//2
metade_esquerda = lista[:meio] # cria uma sublista com a primeira metade
metade_direita = lista[meio:] # cria uma sublista com a segunda metade
mergesort(metade_esquerda)
mergesort(metade_direita)
i=0
j=0
k=0
# Faz a intercalação das duas sublistas ordenadas
while i < len(metade_esquerda) and j < len(metade_direita): # enquanto não chegou ao fim de uma das sublistas
# pega o menor elemento entre os dois elementos atuais das sublistas
# e o coloca na posição atual da lista ordenada
if metade_esquerda[i] < metade_direita[j]:
lista[k]=metade_esquerda[i]
i=i+1
else:
lista[k]=metade_direita[j]
j=j+1
k=k+1
# Uma das sublistas sempre termina antes da outra;
# Os laços a seguir percorrem a sublista inacaba,
# para incluir seus elementos na lista ordenada
while i < len(metade_esquerda):
lista[k]=metade_esquerda[i]
i=i+1
k=k+1
while j < len(metade_direita):
lista[k]=metade_direita[j]
j=j+1
k=k+1
print("Intercalação: ",lista) # imprime a lista apenas para auxiliar o entendimento da função
# Se a sublista tem menos do que 2 elementos,
# então ela já está ordenada a função não precisa
# fazer nada!
############################
# Testa a função de ordenação mergesort()
L = [54,26,93,17,77,31,44,55,20]
print("Lista original:", L)
print("*** Início da ordenação ***")
mergesort(L)
print("*** Fim da ordenação ***")
print("Lista ordenada:", L)
Problema 25.6 (Séries com Números Reais)
Obs.: Este problema corresponde ao exercício 4 da lista de exercícios sobre Funções - Parte 1.
(a) Faça uma função arctan que recebe um número real x $\in [0,1]$ e devolve uma aproximação do arco tangente de x (em radianos) através da série
$$ arctan(x) = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + ... $$
incluindo todos os termos da série até $ |\frac{x^k}{k}| < 0,0001 $.
def arctan(x):
'''
(float) -> float
Função que recebe um número real x, tal que 0 <= x <= 1,
e devolve uma aproximação do arco tangente de x em
radianos.
'''
eps = 0.0001
soma = termo = pot = x
k = 1
while termo >= eps or -termo >= eps:
k += 2
pot *= -x*x
termo = pot/k
soma = soma + termo
return soma
(b) Faça uma função angulo que recebe um ponto de coordenadas cartesianas reais (x,y), com x > 0 e y > 0 e devolve o ângulo formado pelo vetor (x,y) e o eixo horizontal.
Exemplos: Observe a figura abaixo e os ângulos (aproximadas) correspondentes aos pontos marcados.
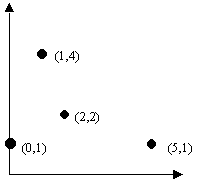
| Ponto | Ângulo |
|---|---|
| (0,1) | 90 graus |
| (2,2) | 45 graus |
| (1,4) | 75 graus |
| (5,1) | 11 graus |
Use a função criada no item (a) no cálculo do ângulo. Note que a função só calcula o arco tangente de números entre 0 e 1, e o valor devolvido é o ângulo em radianos (use o valor $\pi$ = 3.14 radianos = 180 graus).
Para calcular o valor do ângulo $\alpha$ pedido, use a seguinte fórmula:
$$\alpha = \begin{cases} arctan(\frac{y}{x}), & \mbox{caso }y<x \\ \frac{\pi}{2} - arctan(\frac{x}{y}), & \mbox{no caso contrário}\end{cases}$$
PI = 3.14
# Função extra
def graus(x):
'''
(float) -> float
Função que recebe um valor em radianos e
devolve o valor correspondente em graus.
'''
return 180*x/PI
def angulo(x,y):
'''
(float,float) -> float
Função que recebe como entrada um ponto (x,y) e
devolve o ângulo em graus que o vetor (x,y) forma
com o eixo horizontal.
'''
if x == 0 and y == 0:
return -1 # Para (0,0), não há ângulo!
if y < x:
ang = arctan(y/x)
else:
ang = PI/2 - arctan(x/y)
return graus(ang)
(c) Faça um programa que, dados n pontos do primeiro quadrante (x >= 0 e y >= 0) através de suas coordenadas cartesianas, determina o ponto que forma o menor ângulo com o eixo horizontal. Use a função do item anterior.
def main():
n = int(input("Digite quantidade de pontos: "))
angmin = 100 # qualquer valor acima de 90 vale como inicialização
for i in range(1,n+1):
x = float(input("Digite a coordenada x do %do. ponto: " %i))
y = float(input("Digite a coordenada y do %do. ponto: " %i))
ang = angulo(x,y)
if ang == -1:
print("Ponto na origem, será desconsiderado")
elif ang < angmin:
angmin = ang;
xmin = x
ymin = y
print("Ponto de menor ângulo: (%f,%f)" %(xmin,ymin))
print("Menor ângulo: %f graus" %angmin)
# Executa o programa principal
main()