Departamento de Ciência da
Computação - IME - USP
MAC2166 Introdução à Computação
Escola Politécnica - Primeiro Semestre de 2016
Prova 1
QUESTÃO 1
Sejam a, b e c números inteiros
tais
que a ≥ b ≥ c > 0. Sabe-se
que os valores a, b e c são
comprimentos dos lados de um triângulo
se a < b + c.
Suponha que a, b e c são
comprimentos dos lados de um triângulo. Quanto aos ângulos diz-se
que um triângulo é
-
se a2 = b2 + c2;
-
se a2 > b2 + c2;
ou
-
se a2 < b2 + c2.
Quanto aos lados diz-se que um triângulo é
se os três lados têm o mesmo comprimento;
se exatamente dois lados têm o mesmo comprimento; ou
se os três lados têm comprimentos diferentes.
Escreva um programa que lê 3 números inteiros positivos e imprime
uma mensagem indicando se eles são ou não comprimentos dos lados de
um triângulo. No caso deles serem comprimentos de um triângulo o
programa deve ainda imprimir mensagens indicando a
classificação do triângulo quanto aos ângulos e quanto aos lados.
A seguir estão 4 exemplos de execução do programa. A saída do seu
programa deve ser igual às mostradas nos
exemplos.
Os valores em vermelho foram digitados pelo usuário.
Digite um inteiro: 3
Digite um inteiro: 5
Digite um inteiro: 4
São comprimentos dos lados de um triângulo
retângulo
escaleno
Digite um inteiro: 4
Digite um inteiro: 2
Digite um inteiro: 3
São comprimentos dos lados de um triângulo
obtusângulo
escaleno
Digite um inteiro: 4
Digite um inteiro: 3
Digite um inteiro: 4
São comprimentos dos lados de um triângulo
acutângulo
isósceles
Digite um inteiro: 3
Digite um inteiro: 7
Digite um inteiro: 4
Não são comprimentos dos lados de um triângulo
SOLUÇÃO
#
# Solução 1: coloca em a o maior valor
#
def main():
a = int(input("Digite um inteiro: "))
b = int(input("Digite um inteiro: "))
c = int(input("Digite um inteiro: "))
print("%d, %d e %d " %(a, b, c))
# coloque em a o maior dos valores
if b > a and b >= c:
aux = a # a, b = b, a
a = b
b = aux
elif c > a and c > b:
aux = a # a, c = c, a
a = c
c = aux
# indique se a, b e c são comprimentos dos lados de um triângulo
if a >= b + c:
print("Não são comprimentos dos lados de um triângulo")
else:
print("São comprimentos dos lados de um triângulo")
# indique a classificacao quanto aos ângulos
if a*a == b*b + c*c:
print("retângulo")
elif a*a > b*b + c*c:
print("obtusângulo")
else:
print("acutângulo")
# indique a classificacao quanto aos lados
if a == b == c:
print("equilátero")
elif a == b or a == c or b == c:
print("isósceles")
else:
print("escaleno")
#---------------------------------------------------------
main()
#
# Solução 2: utiliza os operadores lógicos _and_ e _or_
#
def main():
a = int(input("Digite um inteiro: "))
b = int(input("Digite um inteiro: "))
c = int(input("Digite um inteiro: "))
print("%d, %d e %d " %(a, b, c))
# indique se a, b e c são comprimentos dos lados de um triângulo
if a >= b + c or b >= a + c or c >= a + b:
print("Não são comprimentos dos lados de um triângulo")
else:
print("São comprimentos dos lados de um triângulo")
# indique a classificacao quanto aos ângulos
if a*a == b*b + c*c or b*b == a*a + c*c or c*c == a*a + b*b:
print("retângulo")
elif a*a > b*b + c*c or b*b > a*a + c*c or c*c > a*a + b*b:
print("obtusângulo")
else:
print("acutângulo")
# indique a classificacao quanto aos lados
if a == b == c:
print("equilátero")
elif a == b or a == c or b == c:
print("isósceles")
else:
print("escaleno")
#-------------------------------------------
main()
QUESTÃO 2
Dizemos que uma sequência com pelo menos 3 números inteiros e sem
elementos consecutivos iguais é um se tem um pedaço
inicial crescente (estritamente) depois
fica decrescente (estritamente) até o final.
[1,2,1] é um pico, pois tem o pedaço inicial crescente [1,2] e depois decresce.
[1,5,3] é um pico, pois tem o pedaço inicial crescente [1,5] e depois decresce.
[2, 5, 10, 46, 25, 12, 7] é um pico, pois tem o pedaço inicial crescente [2, 5, 10, 46] e depois só decresce.
[13, 5, 4, 12, 3, 0, -3, -14] não é um pico, pois o seu pedaço inicial [13, 5] é decrescente.
[6, 7, 8, 9, 10] não é um pico, pois tem apenas um pedaço crescente.
[10, 9, 7, 4] não é um pico, pois tem apenas um pedaço decrescente.
[1, 2, 1, 2, 1, 2, 1] não é um pico, pois depois do pedaço inicial crescente [1, 2] não decresce até o final.
Escreva um programa (= função main()) que lê um
inteiro n, n ≥ 3,
e uma sequência com n números inteiros e imprime uma
mensagem indicando se a sequência é um pico ou não. O seu
programa pode supor, sem verificar, que a
sequência não tem números consecutivos iguais.
A seguir estão 4 exemplos de execução do programa. A saída do seu
programa deve ser igual às mostradas nos exemplos.
Os valores em vermelho foram
digitados pelo usuário.
Digite n: 7
Digite um número: 10
Digite um número: 9
Digite um número: 8
Digite um número: 7
Digite um número: 6
Digite um número: 5
Digite um número: 4
A sequência não é um pico.
Digite n: 5
Digite um número: -2
Digite um número: 6
Digite um número: 12
Digite um número: 24
Digite um número: -1
A sequência é um pico.
Digite n: 6
Digite um número: 2
Digite um número: 5
Digite um número: 10
Digite um número: 25
Digite um número: 30
Digite um número: 45
A sequência não é um pico.
Digite n: 8
Digite um número: 1
Digite um número: 2
Digite um número: 1
Digite um número: 2
Digite um número: 1
Digite um número: 2
Digite um número: 1
Digite um número: 2
A sequência não é um pico.
SOLUÇÃO
#
# Solução 1: usa indicadores de passagem
#
def main():
n = int(input("Digite n: "))
# leia primeiro e segundo números
anterior = int(input("Digite um número: "))
atual = int(input("Digite um número: "))
# verifique se há um pedaço inicial crescente
if anterior < atual:
pico = True # indica que até agora a sequência é um pico
subida = True
else:
pico = False # indica que a sequência não é um pico
# prepara para o início da próxima iteração
anterior = atual
i = 2
while i < n:
atual = int(input("Digite um número: "))
if anterior < atual:
# estamos subindo
if not subida: # subida == False
# se estávamos no meio da descida, não é um pico
pico = False
else:
# aqui vale que anterior > atual, estamos em uma descida
subida = False
anterior = atual
i += 1
# para sequências com apenas um pedaço crescente
if subida: # subida == True
pico = False
# imprime a resposta
if pico: # pico == True
print("A sequência é um pico.")
else:
print("A sequência não é um pico.")
#---------------------------------------------------------
main()
#
# Solução 2: usa contadores de picos e vales
# uma sequência é um pico se possui apenas 1 pico e 0 vales
def main():
n = int(input("Digite n: "))
# leia os dois primeiros número (n >= 3)
anterior = int(input("Digite um número: "))
atual = int(input("Digite um número: "))
# contadores
no_picos = 0 # de picos Λ
no_vales = 0 # de vales ⋁
i = 2 # contador de números lidos
while i < n:
# leia o próximo número
prox = int(input("Digite um número: "))
# verifique se atual é o "centro" de um pico: Λ
if anterior < atual > prox: # anterior < atual and atual > prox
no_picos += 1
# verifique se atual é o "centro" de um "vale": ⋁
elif anterior > atual < prox: # anterior > atual and atual < prox
no_vales += 1
# atualize o papel de anterior e atual para a próxima iteração
anterior = atual
atual = prox
i += 1
if no_picos == 1 and no_vales == 0:
print("A sequência é um pico.")
else:
print("A sequência não é um pico.")
#---------------------------------------------------------
main()
#
# Solução 3: verifica os trechos sobe e desce da sequência
#
def main():
n = int(input("Digite n: "))
# indicadores de passagem
subiu = False # a sequência cresceu no início
desceu = False # a sequência decresceu após um possível crescimento inicial
subiu_novamente = False # após um possível crescimento e decrescimento inícial,
# houve um novo crescimento (=sobrou algum elemento)
# leia primeiro e segundo números
anterior = int(input("Digite um número: "))
atual = int(input("Digite um número: "))
i = 2 # contador de números lidos
# verifique se no inicio há um crescimento
if anterior < atual:
subiu = True
# leia os números enquanto é crescente
while i < n and anterior < atual:
anterior = atual
atual = int(input("Digite um número: "))
i += 1
# verifique se, após um possível crescimento, a sequência descrece
if anterior > atual:
desceu = True
# leia os número enquanto é decrescente
while i < n and anterior > atual:
anterior = atual
atual = int(input("Digite um número: "))
i += 1
# verifique se após um possível crescimento e decrescimento, ha um novo crescimento
if anterior < atual:
subiu_novamente = True
# leitura do possível resto da sequência
while i < n:
atual = int(input("Digite um número: "))
i += 1
# imprime a resposta
if subiu and desceu and not subiu_novamente: # subiu = desceu == True and subiu_novamente == False
print("A sequência é um pico.")
else:
print("A sequência não é um pico.")
#---------------------------------------------------------
main()
QUESTÃO 3
Esta questão consiste na implementação de 3 funções.
Item 3(a)
Suponha que s e c são
inteiros, s ≥ 0
e c ≥ 0,
com o mesmo número de dígitos. Zeros à esquerda são levados em
consideração. Uma mesma posição em que s e c
têm um mesmo dígito é chamada de posição certa.
Por exemplo, se considerarmos inteiros com 3 dígitos, temos que
s = 123 e c = 123 têm 3 posições
certas;
s = 12 (= 012) e c = 123
têm 0 posições certas;
s = 111 e c = 1 (= 001)
têm 1 posição certa;
s = 50 (= 050) e c = 505
têm 0 posições certas; e
s = 708 e s = 8 (= 008) têm 2 posições certas.
Escreva uma função posicoes_certas() como especificada a seguir.
def posicoes_certas(s, c):
'''(int, int) -> int
Recebe dois números inteiros s >= 0 e c >= 0 com 3 dígitos
cada e retorna o número de posições certas de s e c.
Exemplos:
posicoes_certas(467,746) retorna 0
posicoes_certas(123,23) retorna 2
posicoes_certas(1,1) retorna 3
posicoes_certas(1,21) retorna 2
posicoes_certas(21,2) retorna 1
posicoes_certas(21,21) retorna 3
posicoes_certas(321,21) retorna 2
posicoes_certas(0,0) retorna 3
'''
SOLUÇÃO
def posicoes_certas(s, c):
no_certos = 0
i = 0
while i < 3:
if s % 10 == c % 10:
no_certos += 1
s = s // 10
c = c // 10
i = i + 1
return no_certos
Item 3(b)
Suponha que s e c são
inteiros, s ≥ 0
e c ≥ 0,
com o mesmo número de dígitos. Zeros à esquerda são levados em
consideração.
Diremos que pode haver um casamento entre uma
posição de s e uma posição de c se essas
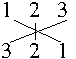
posições têm um mesmo dígito. Por exemplo, se s = 123
e c = 321, então pode haver casamento entre a unidade
de s e a centena de c, a dezena
de s e a dezena de c e a unidade
de s e a centena de c.
O número de dígitos casados entre s
e c é o maior número possível de casamentos entre
posições de s e c em que uma mesma posição
não apareça em dois casamentos (poligamia é proibida). Por
exemplo, se considerarmos inteiros com 3 dígitos, temos que:
Escreva uma função digitos_casados() como especificada a seguir.
def digitos_casados(s, c):
'''(int, int) -> int
Recebe dois números inteiros s >= 0 e c >= 0 com 3 dígitos
cada e retorna o número dígitos casados entre s e c.
Exemplos:
digitos_casados(123,312) retorna 3
digitos_casados(123,31) retorna 2
digitos_casados(123,1) retorna 1
digitos_casados(100,1) retorna 3
digitos_casados(100,102) retorna 2
digitos_casados(2,1) retorna 2
digitos_casados(0,0) retorna 3
digitos_casados(222,1) retorna 0
'''
SOLUÇÃO
def digitos_casados(s, c):
no_casamentos = 0
# obtenha os dígitos do s
s0 = s%10 # unidade
s1 = (s//10)%10 # dezena
s2 = (s//100) # centena, pois tem 3 dígitos
# obtenha os dígitos do c
c0 = c%10 # unidade
c1 = (c//10)%10 # dezena
c2 = c//100 # centena, pois tem 3 dígitos
# conte o número de casamentos
if s0 == c0:
no_casamentos += 1
c0 = -1
elif s0 == c1:
no_casamentos += 1
c1 = -1
elif s0 == c2:
no_casamentos += 1
c2 = -1
if s1 == c0:
no_casamentos += 1
c0 = -1
elif s1 == c1:
no_casamentos += 1
c1 = -1
elif s1 == c2:
no_casamentos += 1
c2 = -1
if s2 == c0 or s2 == c1 or s2 == c2:
no_casamentos += 1
return no_casamentos
Item 3(c)
Escreva um programa (= função main()) que sorteia um
inteiro segredo, segredo ≥ 0,
com 3 dígitos, que deverá ser adivinhado por um jogador. Zeros à
esquerda são considerados.
Em cada tentativa do jogador para adivinhar o inteiro segredo o programa:
lê um inteiro chute digitado pelo jogador, chute ≥ 0, com 3 dígitos, zeros à esquerda são considerados;
imprime o número de posições certas de segredo e chute; e
imprime o número de dígitos casados de segredo e chute.
O programa deve parar assim que o número segredo for adivinhado pelo jogador ou depois de 6 tentativas frustadas. Ao final, o programa deve imprimir uma mensagem informado o número sorteado e se o jogador adivinhou ou não o segredo.
O seu programa deve utilizar a
função posicoes_certas() do item 3(a) e a
função digitos_casados() do item 3(b) . Você pode
utilizar essas funções mesmo que não as tenha feito.
A seguir estão exemplos de 3 execuções do programa. A saída do seu
programa deve ser igual às mostradas nos exemplos.
Os valores em vermelho foram digitados pelo usuário.
1a tentativa
Digite o seu chute: 123
Posições certas = 0
Dígitos casados = 0
2a tentativa
Digite o seu chute: 456
Posições certas = 1
Dígitos casados = 1
3a tentativa
Digite o seu chute: 056
Posições certas = 0
Dígitos casados = 0
4a tentativa
Digite o seu chute: 478
Posições certas = 2
Dígitos casados = 2
5a tentativa
Digite o seu chute: 479
Posições certas = 1
Dígitos casados = 1
6a tentativa
Digite o seu chute: 428
Posições certas = 2
Dígitos casados = 2
Você não adivinhou o segredo 448}
1a tentativa
Digite o seu chute: 123
Posições certas = 0
Dígitos casados = 0
2a tentativa
Digite o seu chute: 456
Posições certas = 1
Dígitos casados = 2
3a tentativa
Digite o seu chute: 457
Posições certas = 1
Dígitos casados = 2
4a tentativa
Digite o seu chute: 548
Posições certas = 0
Dígitos casados = 2
5a tentativa
Digite o seu chute: 954
Posições certas = 0
Dígitos casados = 3
6a tentativa
Digite o seu chute: 495
Posições certas = 3
Dígitos casados = 3
Você adivinhou o segredo 495 em 6 tentativas!
1a tentativa
Digite o seu chute: 1
Posições certas = 1
Dígitos casados = 3
2a tentativa
Digite o seu chute: 010
Posições certas = 1
Dígitos casados = 3
3a tentativa
Digite o seu chute: 100
Posições certas = 3
Dígitos casados = 3
Você adivinhou o segredo 100 em 3 tentativas!
SOLUÇÃO
def main():
'''
Programa que sorteia um número segredo com 3 dígitos, zeros à esquerda
são considerados, que deve ser adivinhado por um jogador.
Em cada tentativa do jogador para adivinhar o segredo o programa pede
ao usuário que digite um número chute com até 3 dígitos e informa ao
usuário quantos dígitos de segredo e chute estão em posição certa
e quantos podem ser casados.
O programa para assim que o número segredo for adivinhado pelo
jogador ou depois de 6 tentativas frustadas.
'''
# sorteie um número de 3 dígitos
segredo = random.randrange(0,1000)
# inicializações
adivinhou = False
no_tentativas = 0
while no_tentativas < 6 and not adivinhou: # adivinhou == False
no_tentativas += 1
print("%da tentativa" %no_tentativas)
chute = int(input("Digite o seu chute: "))
pos_certas = posicoes_certas(segredo, chute)
dig_certos = digitos_casados(segredo, chute)
print("Posições certas = %d" %(pos_certas))
print("Dígitos casados = %d" %(dig_certos))
print()
if segredo == chute:
adivinhou = True
if adivinhou: # adivinhou == True
print("Você adivinhou o segredo %d em %d tentativas!"
%(segredo, no_tentativas))
else:
print("Você não adivinhou o segredo %d" %(segredo))
Last modified: Thu Apr 5 15:58:25 BRT 2016
 ;
; ;
; ou
ou 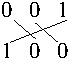 ;
; ou
ou 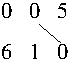 ;
;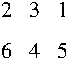 ; e
; e ou
ou 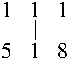 ou
ou 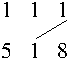 .
.