Resultados e informações sobre a área de pesquisa de Métodos Numéricos e Modelagem de Fluidos Geofísicos, em particular com aplicações em Modelos Atmosféricos. Boa parte desses estudos tem tido financiamento da FAPESP, em particular considerando um Projeto Jovem Pesquisador I e II.
Palestras Selecionadas
Resultados Científicos Selecionados (até 2021)
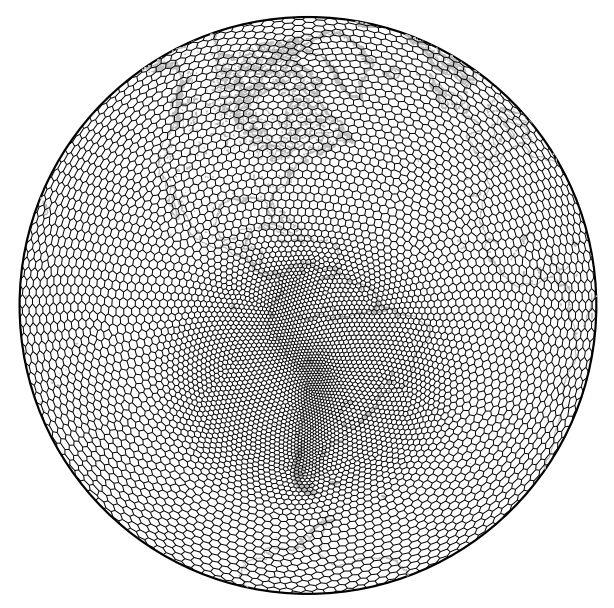
Topography based local spherical Voronoi grid refinement
Desenvolvimento de métodos para melhor captura de fenômenos atmosféricos passando sobre os Andes.
- Santos, L.F. and Peixoto, P.S., 2021. Topography based local spherical Voronoi grid refinement on classical and moist shallow-water finite volume models. Geoscientific Model Development, pp.1-31.
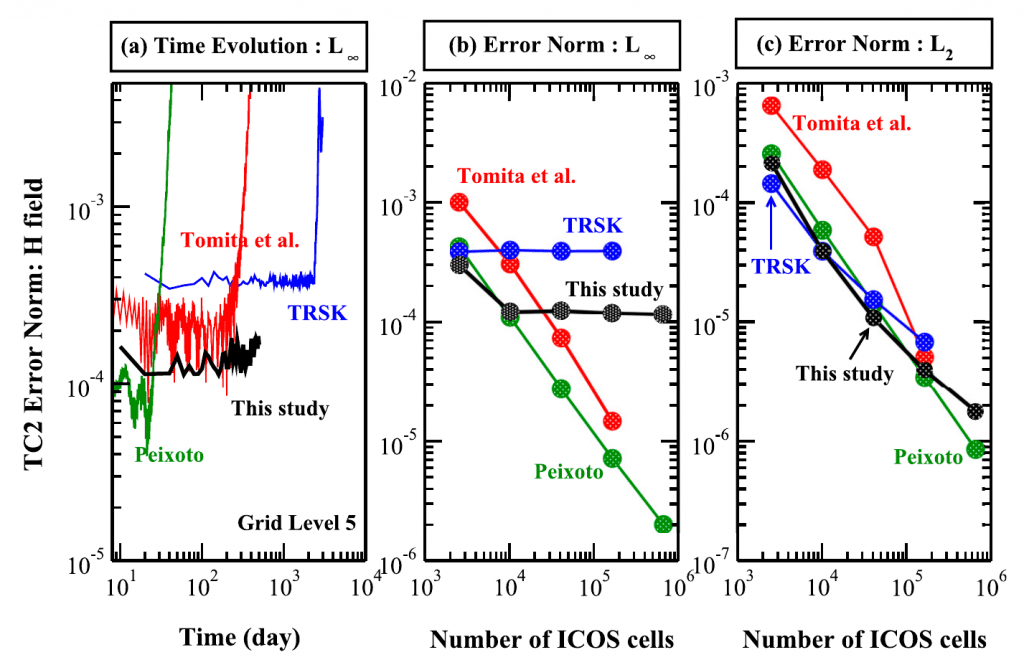
Comparing Numerical Accuracy of Icosahedral A-Grid and C-Grid Schemes in Solving the Shallow-Water Model
Colaboração com pesquisadores da NOAA-USA em uma análise comparativa de métodos de discretização com volumes finitos para malhas icosaédricas atualmente em uso em um modelo americano de previsão do tempo e simulações climáticas (MPAS) e um modelo japonês (NICAM).
- Yu, Y.G., Wang, N., Middlecoff, J., Peixoto, P.S. and Govett, M.W., 2020. Comparing Numerical Accuracy of Icosahedral A-Grid and C-Grid Schemes in Solving the Shallow-Water Model. Monthly Weather Review, 148(10), pp.4009-4033.
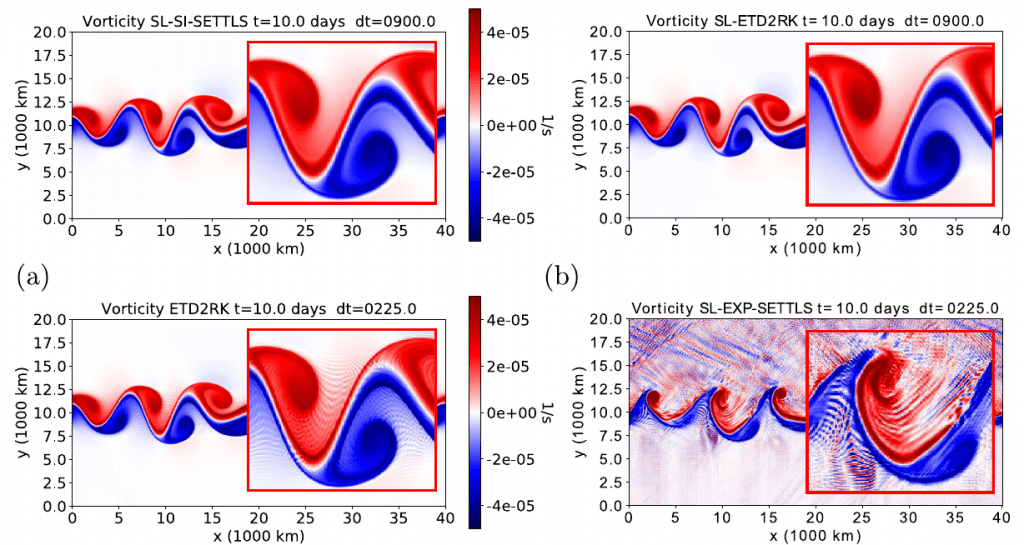
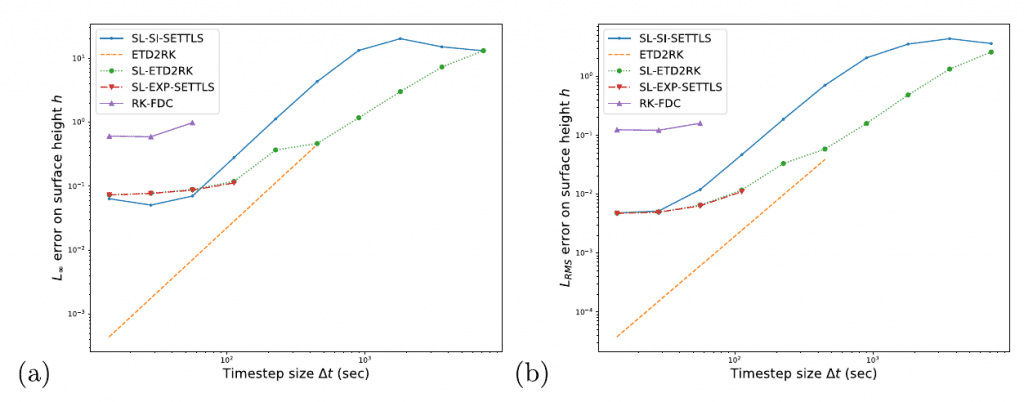
Semi-Lagrangian Exponential Integration with application to the rotating shallow water equations
Propomos neste artigo a junção de classes de métodos: integradores exponenciais e métodos semi-Lagrangianos, resultando em uma nova classe de métodos que permitem passos de tempo grandes em problemas com adveção não linear e operadores lineares rígidos. Trabalho em conjunto com Martin Schreiber (TU Munique).
- Peixoto, P.S. and Schreiber, M., 2019. Semi-Lagrangian Exponential Integration with application to the rotating shallow water equations. SIAM Journal on Scientific Computing, 41(5), pp.B903-B928.
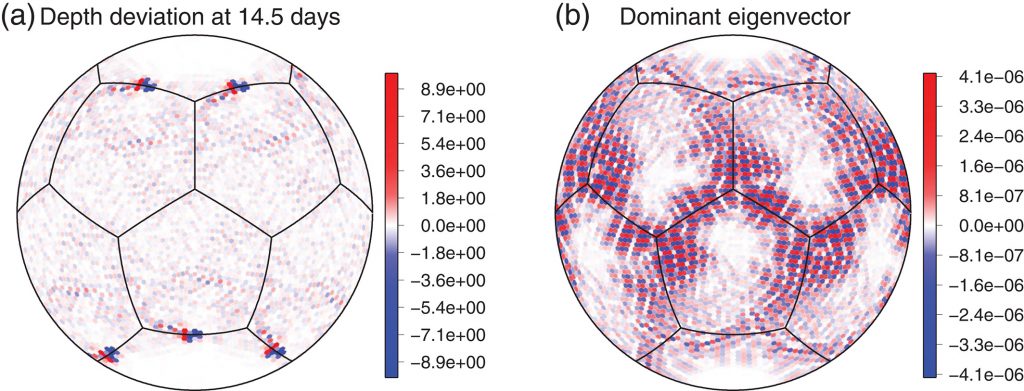
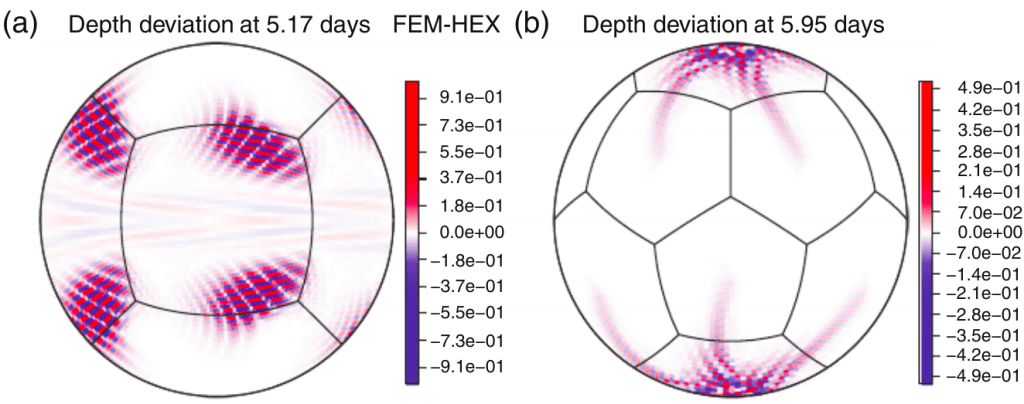
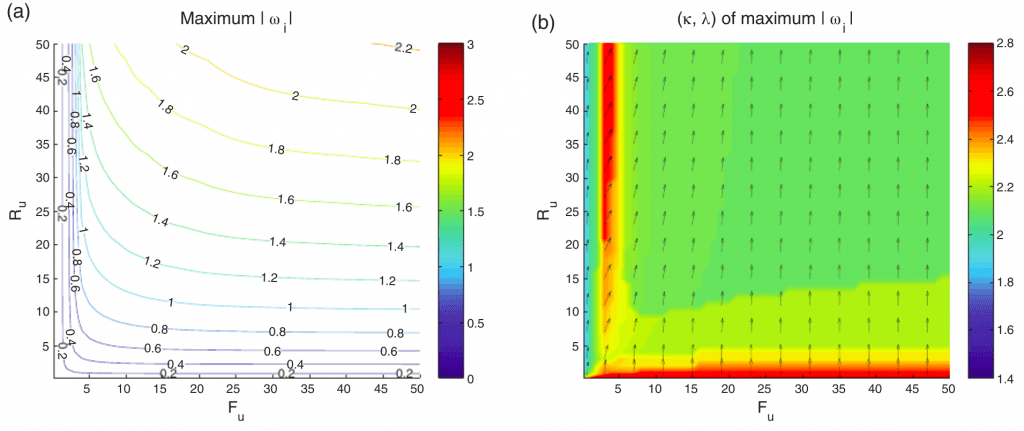
Instabilidade numérica (Hollingsworth) em modelos de águas rasas com alturas equivalentes pequenas
Pesquisa realizada em parceria com os pesquisadores J. Thuburn (U. Exeter – UK) e M. Bell (UK MetOffice) sobre essa intrigantes instabilidade que vem afetando modelos de previsão de tempo modernos.
Peixoto, P.S., Thuburn, J. and Bell, M.J., 2018. Numerical instabilities of spherical shallow‐water models considering small equivalent depths. Quarterly Journal of the Royal Meteorological Society, 144(710), pp.156-171.
Bell, M.J., Peixoto, P.S. and Thuburn, J., 2017. Numerical instabilities of vector‐invariant momentum equations on rectangular C‐grids. Quarterly Journal of the Royal Meteorological Society, 143(702), pp.563-581.
Paralelismo no tempo em advecção não linear
Colaboração com pesquisadores da TU Darmstadt – Germany e Univ. de Exeter- UK na proposição de um método paralelo no tempo usando advecção semi-Lagrangiana.
Schmitt, A., Schreiber, M., Peixoto, P. and Schäfer, M., 2018. A numerical study of a semi-Lagrangian Parareal method applied to the viscous Burgers equation. Computing and Visualization in Science, 19(1-2), pp.45-57.
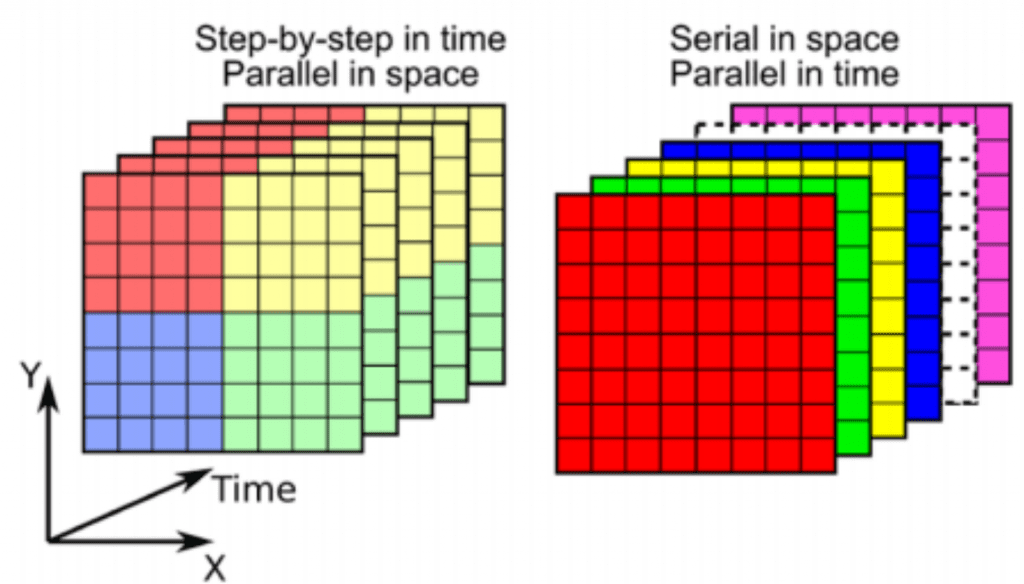
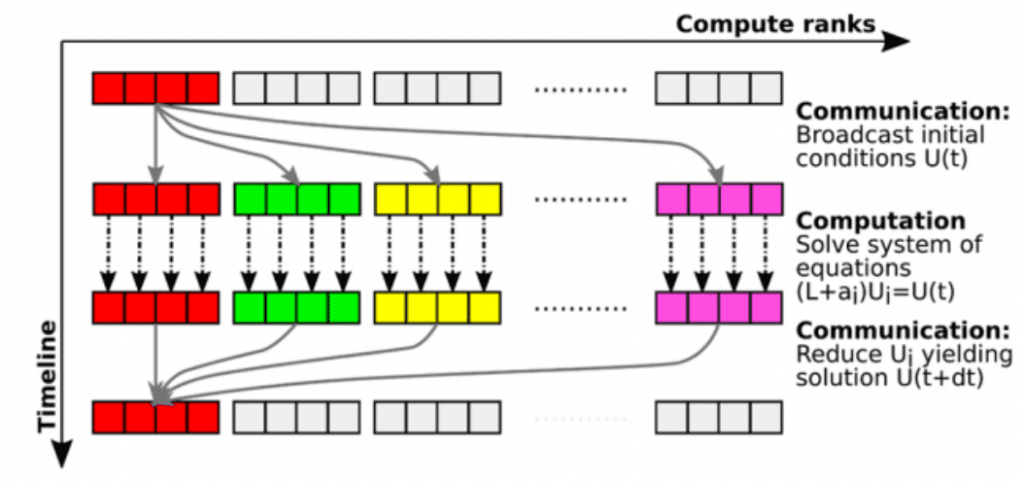
Integrador Exponencial Massivamente Paralelo
Pesquisa em colaboração com pesquisadores da Universidade de Exeter (UK) e do Los Alamos Nat. Lab (USA) visando resolver problemas de EDPs lineares oscilatórios com um integrador exponencial com alto grau de paralelismo.
Schreiber, M., Peixoto, P.S., Haut, T. and Wingate, B., 2018. Beyond spatial scalability limitations with a massively parallel method for linear oscillatory problems. The International Journal of High Performance Computing Applications, 32(6), pp.913-933.
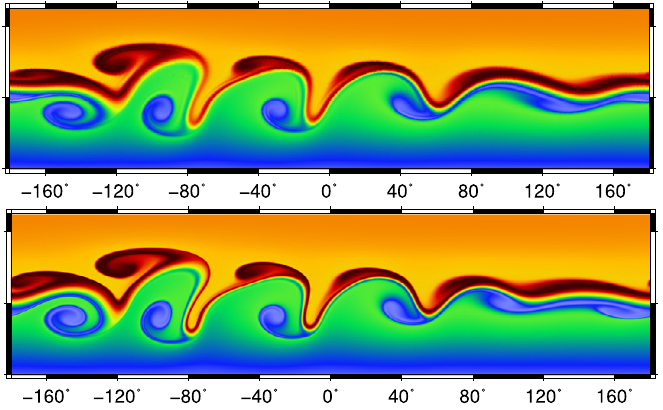
Análise de operadores de métodos de volumes finitos em malhas geodésicas
Investigação sobre os problemas existentes em métodos numéricos atualmente em uso em modelos modernos de previsão de tempo e clima causados por interferência de malha.
Peixoto, P.S., 2016. Accuracy analysis of mimetic finite volume operators on geodesic grids and a consistent alternative. Journal of Computational Physics, 310, pp.127-160.
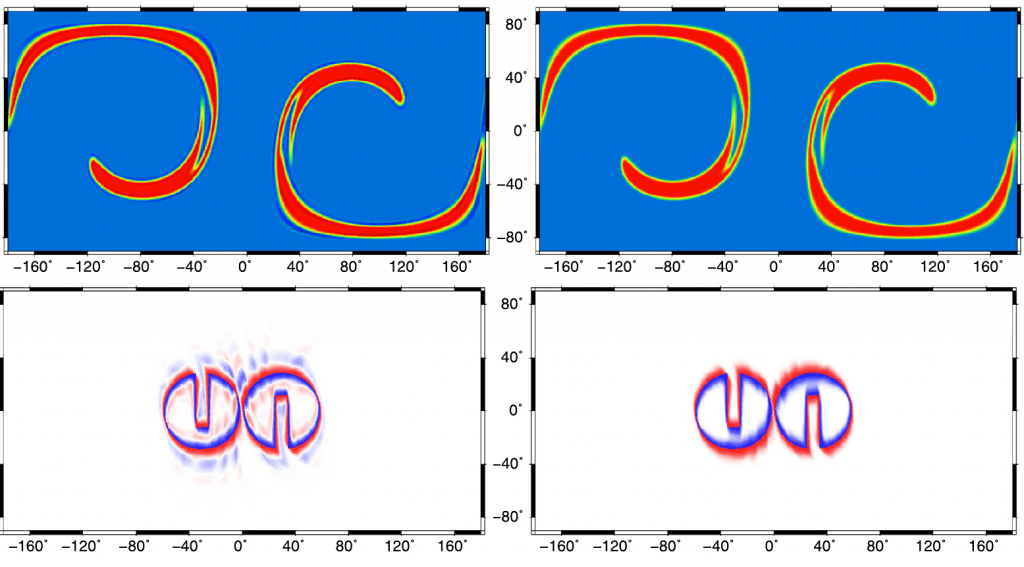
Reconstruções vetoriais em malhas geodésicas
Uma revisão e proposta de métodos para recontrução vetorial em malhas geodésicas icosaédricas para serem usados em advecção semi-Lagrangiana.
Peixoto, P.S. and Barros, S.R., 2014. On vector field reconstructions for semi-Lagrangian transport methods on geodesic staggered grids. Journal of Computational Physics, 273, pp.185-211.
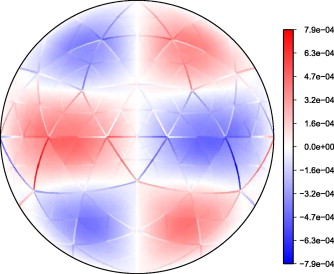
Interferência de malha em malhas geodésicas
Um resultado que explica teoricamente o motivo de observarmos interferências de malhas em modelos de volumes finitos em malhas icosaédricas.
Peixoto, P.S. and Barros, S.R., 2013. Analysis of grid imprinting on geodesic spherical icosahedral grids. Journal of Computational Physics, 237, pp.61-78.
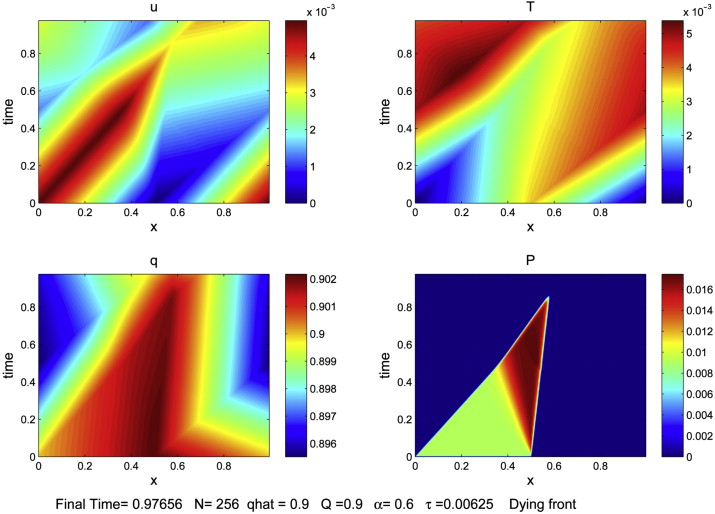
Ondaletas e resolução de equações diferenciais
Uma proposta de método espectral usando ondaletas para advecção não linear e para um modelo frentes de precipitação (chuva).
Barros, S.R. and Peixoto, P.S., 2011. Computational aspects of harmonic wavelet Galerkin methods and an application to a precipitation front propagation model. Computers & Mathematics with Applications, 61(4), pp.1217-1227.