___________________________________________________________________________________________________

Terceira prova de MAP0125 _________________________________________________________________________________________________________________

Cada questão vale dois pontos. Sua nota será a soma das CINCO melhores questões

1. Considere as funções:

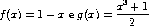
x3 + 1 f (x) = 1- x e g(x) = ------- 2

Encontre numericamente a única soluçao da equação

f(x) = g(x)
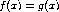(1)
2. Resolva o sistema linear abaixo usando o método da eliminação de Gauss com pivotação.
y + 2z = 4 (2) x + 2y - z = -6 (3) 2x - y + 3z = 13 (4)

3. Uma matriz, A, admite uma decomposição em fatores LU onde a matriz triangular superior U é

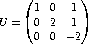
( ) 1 0 1 U = 0 2 1 0 0 -2

Sabendo ainda que a solução do sistema linear

( ) ( ) x1 2 A. x = 5 2 x3 3
(5)
é (x1,x2,x3) = (1, 1, 1), encontre uma matriz triangular inferior, L da decomposição e uma matriz A que satisfaça as condições acima. 4. Faça a tabela de diferenças divididas e ache o polinômio interpolador na forma de Newton da seguinte tabela 1.
x -4 -2 1 2 5
y 11 1 1 5 29

Tabela 1: Questão 5
5. Com relação à tabela 2, achar uma família, p1(x),p2(x),p3(x) de três polinômios ortogonais de grau menor ou igual a dois. Em seguida, encontrar o polinômio de grau menor ou igual a dois que se ajuste a tabela pelo método dos mínimos quadrados.
x -1 0 2
y 1 1 5

Tabela 2: Questão 3
6. Quantas vezes devemos repitir o método de Simpson para obtermos a integral
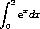
integral 2 exdx 0

com um erro absoluto menos ou igual a 1/10000?