MAC2166 Introdução à Computação

[Edição do 1o. Semestre de 2020]

(Página eternamente minimal e em mutação)

Sandbox

Exercícios de programação

Sinopse das aulas

Fevereiro

[2020-02-20 Thu] Aula de apresentação
[2020-02-27 Thu] Elementos básicos. Dois IDEs:
- CodeBlocks
- Visual Studio Code
  - https://code.visualstudio.com/
Eu usarei o editor de texto Emacs e um terminal, ou farei tudo dentro do Emacs.
- O jogo de Alice e Beto

Março

[2020-03-03 Tue] Primeiros elementos de programação: esqueleto de um programa; comandos de entrada, saída, atribuição e repetição
- Exemplos principais (sandbox): p01.c, p02.c, p03.c
- Duas páginas com dicas relacionadas ao uso da linha de comando no Windows:
  - Como usar o bash no Windows 10: https://www.laptopmag.com/articles/use-bash-shell-windows-10
  - Como chamar o Command Prompt em várias versões do Windows: https://www.digitalcitizen.life/7-ways-launch-command-prompt-windows-7-windows-8
- Alice e Beto novamente. Alice e Beto jogam o seguinte jogo: Alice escolhe dois números distintos do conjunto 1, 2, …, 20. Ela os escreve em dois cartões, digamos A e B, e põe esses cartões sobre uma mesa, virados para baixo, de forma que Beto não consegue ver os números. Beto pode então pedir para ver um dos cartões. Alice vira o cartão que Beto pede para ver, revelando o número naquele cartão. Beto deve então escolher o cartão A ou o cartão B. Ele ganha se ele escolher o cartão com o número maior. Ele perde se ele escolher o cartão com o número menor. Encontre uma estratégia que Beto pode usar para que ele tenha chance de vitória estritamente maior que 50%.

[2020-03-05 Thu] Comandos de seleção
- Exemplos principais: p04.c, p05.c, ex10.c

[2020-03-10 Tue] Testes de igualdade: ==. Operadores / e %
- Exemplos principais: p06.c, p07.c, ex14.c

[2020-03-12 Thu] Comando for e operdores && e ||
- Exemplos principais: p08.c, p09.c, p10.c, ex08.c

[2020-03-17 Tue] A aula será via o Google Hangouts Meet. Vamos ver se esse esquema funciona. Cobriremos nessa aula o que chamamos de "repetições encaixadas" ou "laços encaixados".

Peço que tentem resolver os seguintes problemas:
- Problema 11. Dados um número inteiro N > 0 e uma sequência com N números inteiros não-negativos, determinar o fatorial de cada número da sequência.
- Problema 12 (Exercício 12 da lista de exercícios sobre inteiros). Dados dois inteiros não-negativos, calcular o máximo divisor comum entre eles usando o algoritmo de Euclides.
- Problema 13 (Exercício 7 da lista de exercícios sobre repetições encaixadas). Dados um número inteiro positivo N e uma sequência com N números inteiros positivos, determinar o máximo divisor comum entre eles. Por exemplo, para a sequência 210 84 60 27 seu programa deve imprimir 3.
A URL (link) para a aula será divulgada no quadro de avisos do e-Disciplinas.
[2020-03-19 Thu] A aula será novamente via o Google Hangouts Meet. O tópico dessa aula é o uso de "indicadores de passagem".

Peço que tentem resolver os seguintes problemas:
- Problema 14. Dados um número inteiro positivo N e uma sequência com N números inteiros, verificar se a sequência está em ordem crescente.
- Problema 15 (Exercício 11 da lista de exercícios sobre inteiros). Dado um número inteiro N > 0, verificar se N é primo.
- Problema 16 (Exercício 6 da lista de exercícios sobre repetições encaixadas). Dado um número inteiro N > 1, imprimir sua decomposição em fatores primos, indicando a multiplicidade de cada fator primo de N. Por exemplo, para N = 600, a saída deverá ser
```
fator 2 multiplicidade 3
fator 3 multiplicidade 1
fator 5 multiplicidade 2
```
- Problema extra. Dado um número inteiro N > 0, verificar se este número contém dois dígitos adjacentes iguais.
A URL (link) para a aula será divulgada no quadro de avisos do e-Disciplinas.
[2020-03-24 Tue] Observações administrativas. Para acessar a aula, visite https://meet.google.com/cti-nozf-byz (as aulas da T3 serão em geral nesse endereço). A partir dessa aula, as aulas serão gravadas e disponibilizadas no e-Aulas. Em cada aula, visite o e-Disciplinas para cadastrar sua participação. Esse cadastro será usado para saber o quanto a turma está conseguindo participar dessas aulas online, e não será usado para calcular a frequência de cada aluno. A frequência será (muito provavelmente) calculada a partir dos trabalhos que você entregar.

O EP1 está adiado por uma semana. Os monitores divulgaram seus horários de plantão e formas de acesso.

Este é um bom momento para você ler/reler em detalhe o material dos Capítulos 2 a 12 de Introdução à Ciência da Computação (versão PDF).

Alunos ávidos a refinar seus conhecimentos de C (e algoritmos mais avançados, estudados em uma segunda disciplina de programação), devem consultar o material em https://www.ime.usp.br/~pf/algoritmos/ (veja, em particular, Recursos da linguagem C naquela página).

Aula. Veremos/recordaremos uma miscelânea de construções de C, como constantes simbólicas (#define TRUE 1), prioridade de operadores, abreviaturas (i++; ++i; a += b;), atribuição múltipla (i = j = 0;), atribuição na declaração de variáveis (int i = 5;).

Tentem fazer os seguintes exercícios em preparação para a aula:
- Problema 17 (Exercício 9 da lista de exercícios sobre inteiros). Dados números inteiros positivos $N$, $i$ e $j$, imprimir em ordem crescente os $N$ primeiros naturais que são múltiplos ou de $i$ ou de $j$. Por exemplo, para $N = 6$, $i = 2$ e $j = 3$ a saída deverá ser $0$ $2$ $3$ $4$ $6$ $8$.
- Problema 18. Dados um número inteiro positivo $N$ e uma sequência com $N$ números inteiros, verificar se a sequência é uma progressão aritmética.
- Exercício 5 da lista de exercícios sobre repetições encaixadas. Sabe-se que um número da forma $N^3$ é igual à soma de $N$ ímpares consecutivos. Por exemplo, $1^3 = 1$, $2^3 = 3 + 5$, $3^3 = 7 + 9 + 11$, $4^3 = 13 + 15 + 17 + 19$, etc. Dado $M>0$, determine os ímpares consecutivos cuja soma é igual a $N^3$ para $N$ assumindo valores de $1$ a $M$.
(Gravação desta aula)
[2020-03-26 Thu] Semana de provas da Poli
[2020-03-31 Tue] Semana de provas da Poli

Abril

[2020-04-02 Thu] Não haverá aula
[2020-04-07 Tue] Semana Santa
[2020-04-09 Thu] Semana Santa
[2020-04-14 Tue] A URL da aula será https://meet.google.com/hkd-fxan-zxg (a partir dessa aula, essa será sempre a URL que vamos usar). Espero que todos tenham tido oportunidade de ver https://edisciplinas.usp.br/mod/forum/discuss.php?d=507180

Em particular, espero que todos tenham tido chance de assistir às vídeo-aulas em https://drive.google.com/drive/folders/1VWo-e7UG9fZ5ofco61l4Y-M7e07_-C0c

Visitem também https://www.ime.usp.br/~mksilva/cursos/2020-1/mac2166/

Os tópicos centrais dessa aula serão constantes e variáveis do tipo double; aritmética envolvendo números do tipo double; leitura de números do tipo double (%lf), impressão de expressões do tipo double (%f); conversão de tipos (molduras; casting).

Vamos discutir a resolução dos seguintes problemas.
- Problema 1. Dado um número inteiro $N > 0$ e $N$ notas de provas de MAC2166, calcular a média aritmética das notas.
- Problema 2 (Exercício 2 da lista de exercícios com reais). Dado um número inteiro $N > 0$, determinar o número harmônico $H_N$, dado por \[ H_N = 1 + \frac12 + \frac13 + \frac14 + \dots + \frac1N. \]
- Problema 3 (Exercício 3 da lista de exercícios com reais). Os pontos $(x,y)$ que pertencem à figura $H$ abaixo são aqueles tais que $x\geq0$, $y\geq0$ e $x^2+y^2\leq1$.
  
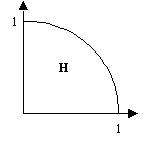
  Dado um número inteiro $N>0$ e as coordenadas de $N$ pontos reais $(x,y)$, imprima, para cada ponto, se ele pertence ou não a $H$.
- Problema extra. Dado um número inteiro $N>0$, calcular o valor da soma \[ S_N=\frac1N+\frac2{N-1}+\frac3{N-2}+\dots+\frac N1. \]
[2020-04-16 Thu] A URL da aula será https://meet.google.com/hkd-fxan-zxg.

Vamos continuar a estudar exemplos envolvendo "números reais" (doubles). Vamos discutir a resolução dos seguintes problemas.
- Problema 4. Dado um número real $x$ e um número real $\varepsilon>0$, calcular uma aproximação de $e^x$ através da seguinte série infinita \[ e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \dots + \frac{x^k}{k!} + \dots \] Inclua na aproximação todos os termos até o primeiro de valor absoluto (módulo) menor do que $\varepsilon$.
- Problema 5 (Exercício 7 da lista de exercícios com reais). Dados $x$ real e um número inteiro $n > 0$, calcular uma aproximação para $\sin x$ através dos $n$ primeiros termos da seguinte série \[ \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \dots + (-1)^k\frac{x^{2k+1}}{(2k+1)!} + \dots \] Compare com os resultados de sua calculadora para diferentes valores de $n$!
- Problema extra. Dado um número real $x$ tal que $0\leq x\leq1$, calcular uma aproximação do arco tangente de $x$ (em radianos) através da série infinita \[ \arctan(x) = x - \frac{x^3}3 + \frac{x^5}5 - \frac{x^7}7 + \dots \] incluindo todos os termos da série até que $|x^k/k|<0.0001$.
- Problema extra. Dado um número real $x>0$, podemos calcular uma aproximação da raiz quadrada de $x$ através da sequência dada por \[ r_0 = x \] e, para $n>0$, \[ r_n =\frac12\left(r_{n-1}+\frac x{r_{n-1}}\right). \] De fato, prova-se que essa sequência de números $r_n$ converge para $\sqrt x$ quando $n\to\infty$.
  
  Use este fato para encontrar uma aproximação de $\sqrt x$. Implemente uma "boa regra de parada".
[2020-04-21 Tue] Tiradentes
[2020-04-23 Thu] A URL da aula será https://meet.google.com/hkd-fxan-zxg. Vamos estudar funções, protótipos de funções, estruturas de funções, e passagem de parâmetros. Vamos discutir a resolução dos seguintes problemas.
- Problema 6. Dados um número real $x$ e números inteiros $a$ e $b$ não-negativos, calcule e imprima os valores das expressões $S=(1+x)^a(1+x)^b$ e $T=(1+x)^{a+b}$. Não use funções.
- Problema 7. Resolva o Problema 6 novamente, usando funções. Mais precisamente, implemente uma função para calcular potências com o seguinte protótipo:
```
double potencia(double x, int n);
```
  Sua função potencia() deve receber um número real $x$ e um inteiro não-negativo $n$ e deve devolver $x^n$. Use esta função para resolver o Problema 6 novamente.
- Problema 8. Sejam $a$ e $b$ dois números naturais. Lembre que \[ {a\choose b}={a!\over b!(a-b)!}={1\over b!}a(a-1)\dots(a-b+1) \] conta o número de subconjuntos de cardinalidade $b$ de um conjunto de cardinalidade $a$. Lembre também que esses coeficientes binomiais aparecem na expansão de $(1+x)^n$.
  - Escreva uma função que recebe um natural $n$ e devolve $n!$.
  - Faça uma função que recebe dois números naturais $a$ e $b$ e, usando a função do item anterior, calcula $a\choose b$.
  - Pergunta. Por que o uso da identidade $a!/(a-b)!=a(a-1)\dots(a-b+1)$ pode melhorar sua função do item anterior? A expressão $a(a-1)\dots(a-b+1)$ é às vezes denotada $(a)_b$ (lê-se "$a$ fatorial decrescente $b$").
  - Faça um programa que lê um número inteiro $n\geq0$ e imprime os coeficientes da expansão de $(1+x)^n$.
- Problema extra. Faça uma função que recebe um número inteiro $n>1$ e devolve $1$ se $n$ é primo e devolve $0$ caso contrário. Faça um programa que lê um número inteiro $m$ e verifica se $m$ pode ser escrito como $p+q$ com $p$ e $q$ primos.
  
  Para aqueles com inclinação matemática. Leia sobre a Conjectura de Goldbach aqui.
- Problema extra. Usando a função sqrt(x) da biblioteca matemática math da linguagem C, escreva uma função que recebe dois pontos no plano através de suas coordenadas cartesianas e devolve a distância entre os pontos. Escreva um programa que lê um número inteiro $n>0$, as coordenadas de um ponto $P_0$ e uma sequência de $n$ pontos $P_1,\dots,P_n$ e determina um ponto da sequência mais próximo do ponto $P_0$.
- Observação. Esta observação não tem a ver diretamente com essa disciplina, mas aqueles com interesses matemáticos vão apreciar. O Problema 6 acima sugere uma prova da seguinte identidade envolvendo coeficientes binomiais, conhecida como a identidade de Vandermonde: para todo inteiro $k\geq0$, vale que \[ \sum_{i+j=k}{a\choose i}{b\choose j}={a+b\choose k} \] (do lado esquerdo, devem ser considerados todos os pares de naturais $i$ e $j$ com $i+j=k$). Você enxerga essa prova?
[2020-04-28 Tue] A URL da aula será https://meet.google.com/hkd-fxan-zxg. Vamos estudar passagem de endereço como parâmetro (passagem de variáveis "por referência").
- Problema 9. Escreva uma função com protótipo
```
int Bhaskara(double a, double b, double c, double *r1, double *r2);
```
  que recebe três reais como parâmetros representando os coeficientes da equação $ax^2 + bx + c = 0$ e devolve $1$ se a equação tem raízes reais e devolve $0$ caso contrário. Ademais, Bhaskara() deve devolver em *r1 e *r2 as raízes reais da equação, quando existem. Finalmente, escreva um programa que lê números reais $a$, $b$, e $c$ e, usando a função acima, imprime as raízes reais $r_1$ e $r_2$ da equação $q(x)=0$ onde $q(x) = ax^2 + bx + c$. Seu programa deve também imprimir $q(r_1)$ e $q(r_2)$.
- Problema 10. Escreva uma função com protótipo
```
int divide_um(int *m, int *n, int d);
```
  que recebe três inteiros positivos como parâmetros e devolve $1$ se $d$ divide pelo menos um entre $*m$ e $*n$, e devolve $0$ caso contrário. Fora isso, se $d$ divide $*m$, divide_um divide $*m$ por $d$, e o mesmo para $*n$. Finalmente, escreva um programa que lê dois inteiros positivos $m$ e $n$ e calcula, usando a função acima, o mínimo múltiplo comum entre $m$ e $n$.
- Problema extra. Um string (isto é, uma cadeia de caracteres) é um palíndromo se lido da direita para a esquerda ou da esquerda para a direita ele é o mesmo string. Um inteiro $N$ é um palíndromo se sua representação na base $10$ é um palíndromo. Exemplos:
```
567765 e 32423 são palíndromos
567675 não é palíndromo
"Socorram-me subi no ônibus em Marrocos" (ignorando espaços, acentos, maiúsculas/minúsculas)
"Oto come doce seco de mocotó"
"A diva em Argel alegra-me a vida"
```
  Escreva uma função que recebe um inteiro $N>0$ e devolve seu primeiro dígito, seu último dígito e altera o valor de $N$ removendo seu primeiro e último dígitos. Exemplos:
  
  $N$ primeiro dígito último dígito novo $N$
  
  732 7 2 3
  
  14738 1 8 473
  
  1010 1 0 1
  
  78 7 8 0
  
  7 7 7 0
  
  Escreva um programa que recebe um inteiro positivo $N$ e verifica se $N$ é palíndromo. Suponha que $N$ não contenha o dígito $0$.
[2020-04-30 Thu] A URL da aula será https://meet.google.com/hkd-fxan-zxg. Vamos continuar a estudar funções.
- Problema 11 (Exercício 2 da lista de exercícios com funções II). Escreva um programa que, dadas duas datas $d_0/m_0/y_0$ e $d_1/m_1/y_1$, imprime o número de dias entre essas datas (por simplicidade, suponha que a primeira data é anterior à segunda). Para escrever esse programa escreva funções com os seguintes protótipos:
```
int numero_de_dias(int d0, int m0, int y0, int d1, int m1, int y1);
int datas_cmp(int d0, int m0, int y0, int d1, int m1, int y1);
int valida(int d, int m, int y);
int bissexto(int y);
void dia_seguinte(int *d, int *m, int *y);
```
  Com a função numero_de_dias() escrita, basta seu main() conter
```
printf("Numero de dias entre %d/%d/%d e %d/%d/%d: %d\n",
       d0, m0, y0, d1, m1, y1, numero_de_dias(d0, m0, y0, d1, m1, y1));
```
  A função datas_cmp() deve devolver $-1$ se $d_0/m_0/y_0$ é anterior a $d_1/m_1/y_1$, deve devolver $1$ se $d_0/m_0/y_0$ é posterior a $d_1/m_1/y_1$ e deve devolver $0$ se as datas são iguais. A função valida() deve devolver TRUE se seu argumento representa uma data válida e deve devolver FALSE caso contrário. A função bissexto() deve devolver TRUE se seu argumento é um ano bissexto e deve devolver FALSE caso contrário. Um ano $y$ é bissexto se ele for múltiplo de $400$ ou se ele for múltiplo de $4$ mas não for múltiplo de $100$. Finalmente, dia_seguinte() deve atualizar seus argumentos para representar o dia seguinte.
- Problema extra. Uma tripla de naturais $(a, b, c)$ é uma tripla pitagórica se $a^2+b^2=c^2$. Ademais, uma tripla pitagórica é primitiva se $a$, $b$ e $c$ tem máximo divisor comum $1$. Por exemplo, todos conhecem a tripla pitagórica $(3,4,5)$, que é uma tripla primitiva. Euclides encontrou uma forma de gerar todas as triplas pitagóricas primitivas. Basta considerar todos os naturais $m$ e $n$ com $m>n$ e definir \[ a=m^2-n^2, \] \[ b=2mn \] e \[ c=m^2+n^2. \] Tais $a$, $b$ e $c$ formam uma tripla pitagórica, e ela é primitiva se e só se $m$ e $n$ são primos entre si e são de paridade diferente. Veja, por exemplo, https://pt.wikipedia.org/wiki/Terno_pitagórico. Escreva um programa que recebe $M$ como entrada e gera todas as triplas pitagóricas primitivas a partir de $m$ e $n$ com ambos $m$ e $n\leq M$. Para resolver esse exercício, escreva uma função de protótipo
```
int pitagorico_primitivo(int m, int n, int *a, int *b, int *c);
```
  que devolve a tripla pitagórica correspondente ao par $(m,n)$ em $(a,b,c)$. Ademais, pitagorico_primitivo() deve devolver TRUE se a tripla devolvida $(a,b,c)$ é primitiva e FALSE caso contrário.

\(N\)	primeiro dígito	último dígito	novo \(N\)
732	7	2	3
14738	1	8	473
1010	1	0	1
78	7	8	0
7	7	7	0

Maio

[2020-05-05 Tue] A URL da aula será https://meet.google.com/hkd-fxan-zxg. Veremos exemplos envolvendo o tipo char, para manipulação de caracteres. Vamos também encontrar um outro tipo de laço: o do-while. Vamos supor que vocês já tiveram oportunidade de estudar o material coberto nas aulas do professor Marcel:

https://drive.google.com/drive/folders/1oA6TtJJD7O4V8l92Wv1PJLFpr4GPrYL5
- Problema 12. Dada uma sequência de caracteres alfanuméricos (isto é, letras A-Za-z e dígitos 0-9) e espaços, seguida pelo caractere '.', determine quantos caracteres há na sequência. Por exemplo, para a entrada "O ponto nao conta.", a resposta deve ser $17$.
- Problema 13. Dada uma sequência de caracteres alfanuméricos (isto é, letras A-Za-z e dígitos 0-9) e espaços, seguida por '.', determine a frequência de vogais na entrada. Por exemplo, para a entrada "Determine quantas vogais tem essa frase.", a resposta deve ser $15/34=0.441176\dots$ ($15\text{ vogais}/34\text{ letras}$).
- Problema 14. Dada uma sequência de caracteres alfanuméricos (isto é, letras A-Za-z e dígitos 0-9) e espaços, seguida por '.', determine o número de caracteres que há na sequência e determine o número de palavras que há na sequência. Por exemplo, na entrada "O voo GOL547 saiu com 10 passageiros." há $36$ caracteres e $7$ palavras.
- Problema 15. Dada uma sequência de caracteres alfanuméricos (isto é, letras A-Za-z e dígitos 0-9) e espaços, seguida por '.', determine o comprimento de uma palavra mais longa da entrada. Experimente seu programa na entrada "O voo GOL547 saiu com 10 passageiros."
- Problema extra. Dada uma sequência de caracteres alfanuméricos (isto é, letras A-Za-z e dígitos 0-9) e espaços, seguida por '.', determine quantas letras minúsculas e maiúsculas ocorrem.
- Observação. Há em C uma biblioteca com algumas funções simples para a manipulação de caracteres (ctype). Em MAC2166, quando explicitamente especificado, você pode usar ctype em seus programas. Nos exercícios dessa aula, não use ctype.

[2020-05-07 Thu] Como sempre, a URL da aula será https://meet.google.com/hkd-fxan-zxg. Discutiremos os seguintes exercícios.
- Problema 16. Escreva um programa que leia uma sequência de caracteres terminada por '$' e que imprima se a sequência de caracteres corresponde a um número inteiro ou não e, neste caso, qual número. Exemplos:
  
  Entrada Saída
  
  32456$ Integer 32456
  
  -12345$ Integer -12345
  
  123AB$ Not an integer
  
  $ Not an integer
  
  -$ Not an integer
  
  Brinde: altere seu programa para permitir entradas da forma +1234$ (a saída deve ser Integer 1234).
- Problema 17. Escreva uma função de protótipo
```
int converta(char *ch);
```
  que recebe um caractere *ch e devolve $1$ se *ch for um caractere alfanumérico (A-Za-z ou 0-9) ou um "whitespace"/"espaço em branco" (isto é, ' ', '\n' ou '\t' (caractere TAB)) e devolve $0$ caso contrário. Além disso, no caso de *ch ser uma letra em a-z, sua função deve converter *ch para maiúscula. No caso de *ch ser um whitespace, sua função deve converter *ch para ' '. Mantenha *ch inalterado em todos os outros casos.
  
  Escreva um programa que leia uma sequência de caracteres alfanuméricos, whitespaces e sinais de pontuação (diferentes de '$'), terminada por '$', e que imprima a entrada convertida para maiúsculas, eliminando os caracteres que não forem alfanuméricos ou whitespaces e transformando todos os whitespaces para ' '. (Seu programa deve imprimir um '\n' no fim de sua saída.)
  
  Por exemplo, com a entrada
```
caracteres
alfanumericos, whitespaces e
sinais de pontuacao$
```
  seu programa deve ter a saída
```
CARACTERES ALFANUMERICOS WHITESPACES E SINAIS DE PONTUACAO
```
- Problema extra. A Cifra de César é uma técnica de criptografia simples em que cada letra do alfabeto é substituída pela letra deslocada de um valor secreto $d>0$. Por exemplo, se $d=5$, 'A' é substituído por 'F', 'B' por 'G', 'C' por 'H' e assim por diante, até 'U' ser substituído por 'Z', 'V' por 'A', 'W' por 'B', etc. Há referências históricas que mostram que o imperador romano comunicava-se com seus generais usando este esquema para evitar que as mensagens fossem descobertas por inimigos. Veja https://en.wikipedia.org/wiki/Caesar_cipher
  
  Escreva uma função de protótipo
```
int cesar(char *ch, int d);
```
  que recebe um caractere *ch e devolve $1$ se *ch for um caractere alfanumérico ou um whitespace (veja o Problema 17) e devolve $0$ caso contrário.
  
  Além disso, no caso de *ch ser uma letra em A-Za-z, sua função deve deslocar *ch de $d$ unidades ciclicamente, como mostrado no exemplo (mantendo letras maiúscula/letras minúscula). No caso de *ch ser um whitespace, sua função deve converter *ch para ' '.
  
  Escreva um programa que receba um inteiro $d$ na linha de comando e leia uma sequência de caracteres alfanuméricos, whitespaces e sinais de pontuação (diferentes de '$'), terminada por '$', e que imprima a entrada codificada pela cifra de César com parâmetro $d$. Na saída de seu programa, os caracteres que não forem alfanuméricos ou whitespaces devem ser eliminados e os whitespaces devem ser convertidos para ' '. (Seu programa deve imprimir um '\n' no fim de sua saída.)
  
  Por exemplo, com $d=5$ e a entrada
```
As armas e os barões assinalados,
Que da ocidental praia Lusitana,$    
```
  seu programa deve ter a saída
```
Fx fwrfx j tx gfwjx fxxnsfqfitx Vzj if thnijsyfq uwfnf Qzxnyfsf
```
- Problema extra. Execute seu programa do problema extra acima para $d=-1$. Ele funciona? Se ele não funcionar, altere-o levemente para que ele funcione.
- Problema extra. Decodifique
```
Wx vnrx mx ljvrwqx crwqj dvj ynmaj Crwqj dvj ynmaj wx vnrx mx ljvrwqx Crwqj dvj ynmaj Wx vnrx mx ljvrwqx crwqj dvj ynmaj  Wdwlj vn nbzdnlnanr mnbbn jlxwcnlrvnwcx Wj ermj mn vrwqjb ancrwjb cx ojcrpjmjb Wdwlj vn nbzdnlnanr zdn wx vnrx mx ljvrwqx Crwqj dvj ynmaj Crwqj dvj ynmaj wx vnrx mx ljvrwqx Wx vnrx mx ljvrwqx crwqj dvj ynmaj
```
[2020-05-12 Tue] Como sempre, a URL da aula será https://meet.google.com/hkd-fxan-zxg. Discutiremos os seguintes exercícios.
- Simulação. Simule a execução do programa em https://www.ime.usp.br/~yoshi/2020i/mac2166/sandbox/2020.05.12/simulacao.c, destacando sua saída (tudo que é impresso pelos printf()).
- Decodificação da Cifra de César. Ficou como exercício decodificar
```
Wx vnrx mx ljvrwqx crwqj...
```
  Como você faria isso de forma automática/semiautomática?
- Problema 15. Você fez o Problema 15?
- Revisitação do Problema 11. Escreva um programa que recebe uma data como entrada e devolve o dia da semana daquela data. Por exemplo, com a entrada 12 5 2020 (12/5/2020), seu programa deve imprimir "3a feira". No calendário que é de uso comum hoje, o Calendário Gregoriano, que começou no dia 15/10/1582, o dia 15/10/1582 foi uma 6a feira. Seu programa deve funcionar para datas iguais ou posteriores a 15/10/1582.
- Sexta-feira 13. Escreva um programa que, dada uma data, descobre qual é a próxima ocorrência de uma "6a feira 13" após aquela data.
- Primeiro de janeiro. Qual é o dia da semana mais provável para o dia primeiro de janeiro? (O calendário gregoriano repete-se a cada $400$ anos.)
- Cifra de César com $d$ negativo. Execute seu programa para a Cifra de César para $d$ negativo. Ele funciona? Se ele não funcionar, altere-o levemente para que ele funcione.
[2020-05-14 Thu] Como sempre, a URL da aula será https://meet.google.com/hkd-fxan-zxg. Passamos agora a estudar o uso de arrays ("vetores") em C.
- Problema 1. Dados $0 < N\leq1000$ e $N$ notas de alunos de MAC2166 (números entre $0.0$ e $10.0$), imprima quantos alunos tiveram nota maior ou igual à média dessas $N$ notas.
- Problema 2. Dado um inteiro $N>0$ e uma sequência de $N$ lançamentos de uma roleta (números inteiros no intervalo $[0,36]$), calcular a frequência de cada número.
- Problema 3. Dados dois números positivos $0 < M\leq1000$ e $0 < N\leq1000$ e duas sequências crescentes com $M$ e $N$ números inteiros, obter uma única sequência crescente contendo todos os elementos das sequências originais (esta sequência deve portanto ter $M+N$ elementos).
- Problema extra. Dados um inteiro $0 < N\leq1000$ e uma sequência de $N$ números inteiros, imprimir a sequência eliminando as repetições.
[2020-05-19 Tue] Como sempre, a URL da aula será https://meet.google.com/hkd-fxan-zxg. Faremos alguns exercícios envolvendo o uso de arrays "bidimensionais" ("matrizes") em C.
- Problema 4. Dado um inteiro $0 < N\leq100$ e uma matriz inteira $A=A_{N\times N}$, verifique se $A$ é simétrica.
- Problema 5. Dado um inteiro $0 < N\leq100$ e uma matriz inteira $A=A_{N\times N}$, verifique se a matriz $A$ tem uma linha, coluna ou diagonal composta apenas por zeros.
- Problema 6. Dados inteiros $0 < L\leq100$, $0 < M\leq100$ e $0 < N\leq100$ e duas matrizes reais $A=A_{L\times M}$ e $B=B_{M\times N}$, calcule a matriz $C=AB$ (o produto matricial de $A$ e $B$).
- Problema extra. Dados inteiros $0 \leq N\leq33$ e $q > 0$, imprima as primeiras $N+1$ linhas do triângulo de Pascal (visite https://en.wikipedia.org/wiki/Pascal's_triangle) e depois imprima o mesmo triângulo de Pascal módulo $q$ (isto é, substitua cada valor pelo resto da divisão desse valor por $q$; experimente $q=2$).
- Problema extra. Um jogo de palavras cruzadas pode ser representado por uma matriz $A_{M\times N}$, onde cada posição da matriz corresponde a um quadrado do jogo, sendo que $0$ indica um quadrado branco e $-1$ indica um quadrado preto. Indique na matriz as posições que são início de palavras horizontais e/ou verticais nos quadrados correspondentes (substituindo os zeros), considerando que uma palavra deve ter pelo menos duas letras. Para isso, numere consecutivamente tais posições. Segue um exemplo.
```
Entrada:

 0 -1  0 -1 -1  0 -1  0
 0  0  0  0 -1  0  0  0 
 0  0 -1 -1  0  0 -1  0
-1  0  0  0  0 -1  0  0 
 0  0 -1  0  0  0 -1 -1

Saída:

 1 -1  2 -1 -1  3 -1  4
 5  6  0  0 -1  7  0  0 
 8  0 -1 -1  9  0 -1  0
-1 10  0 11  0 -1 12  0 
13  0 -1 14  0  0 -1 -1
```
[2020-05-21 Thu] Não haverá aula
[2020-05-26 Tue] Como sempre, a URL da aula será https://meet.google.com/hkd-fxan-zxg. O tópico dessa aula será o uso de vetores e matrizes em funções. Para os conceitos dessa aula, veja https://drive.google.com/drive/u/1/folders/1z40ycKsfGqV5N5MDFAKR0EEFIhzqdL4V. Discutiremos os seguintes problemas nessa aula.
- Problema 7. Escreva uma função de protótipo
```
int indice(int v[], int N, int x); 
```
  que recebe um vetor $v$ com $N$ elementos inteiros e um inteiro $x$, e devolve, caso exista, um índice $i$ em que o valor $x$ ocorre em $v$ (isto é, $v[i]=x$) e devolve $-1$ se $x$ não ocorre em $v$. (Veremos aqui o uso de "sentinelas".)
- Problema 8. Escreva um programa que lê uma sequência de inteiros não-nulos terminada por $0$, e que imprime os elementos dessa sequência, eliminando as repetições. Suponha que a sequência conterá no máximo $1000$ elementos distintos (mas não sabemos quantos elementos ela tem no total, se contamos as repetições). Use a função do problema anterior. (Veja o segundo problema extra do dia [2020-05-14 Thu].)
- Problema 9 (Exercício 1 da lista de exercícios com funções III). Um conjunto $S$ pode ser representado por um vetor $s$ da seguinte forma: armazenamos em $s[0]$ a cardinalidade do conjunto $S$ e armazenamos em $s[1]$, $s[2]$, $\dots$ os elementos do conjunto.
  - Escreva uma função de protótipo
```
void intersecao(int a[], int b[], int c[]);
```
    que recebe dois conjuntos armazenados nos vetores $a$ e $b$ e devolve em $c$ a interseção desses conjuntos. Lembre que $c[0]$ deve conter a cardinalidade da interseção.
  - Escreva um programa que lê um inteiro $N$ e uma sequência de $N$ conjuntos inteiros com no máximo $1000$ cada, dados pelo seu tamanho e os elementos que os compõem, e constroi e imprime o conjunto interseção de todos os conjuntos dados.
- Problema extra. Um polinômio de uma variável com coeficientes inteiros pode ser representado por um vetor inteiro e um inteiro (o grau do polinômio). Escreva funções para ler e imprimir polinômios inteiros. Escreva uma funções para somar e multiplicar polinômios inteiros. Escreva uma calculadora (de duas operações) para manipular polinômios inteiros.

Entrada	Saída
`32456$`	`Integer 32456`
`-12345$`	`Integer -12345`
`123AB$`	`Not an integer`
`$`	`Not an integer`
`-$`	`Not an integer`

[2020-05-28 Thu] Não haverá aula

Junho

[2020-06-02 Tue] Não haverá aula
[2020-06-04 Thu] Como sempre, a URL da aula será https://meet.google.com/hkd-fxan-zxg. No começo da aula, vamos discutir brevemente o EP3. Faremos uma discussão mais detalhada do EP3 na aula de 3a. feira, dia 9/6/2020. O tópico dessa aula será o uso de matrizes em funções. Discutiremos os seguintes problemas nessa aula.
- Problema 10 (Minesweeper). Neste exercício, queremos obter o tabuleiro de um campo minado, supondo que sabemos onde estão as minas. Vamos supor que nossos tabuleiros têm no máximo MMAX linhas e NMAX colunas.
  - Escreva uma função com protótipo
```
int conte_minas(int A[][NMAX + 2], int i, int j);
```
    que recebe como parâmetros uma matriz inteira $A=A_{M\times N}$, e uma posição $(i,j)$ livre da matriz $A$, e devolve o número de posições ao redor da posição $(i,j)$ que contém o valor $-1$ (uma mina), assumindo que a matriz tem uma moldura com $-2$.
  - Escreva um programa que lê dois inteiros $M$ e $N$, e uma matriz $A=A_{M\times N}$ com entradas $0$ (posições livres) e $-1$ (minas). Utilizando a função do item anterior, o programa deve computar e imprimir a quantidade de minas ao redor de cada posição livre da matriz.
- Problema 11 (Exercício 14 da lista de exercícios com funções III). Dizemos que uma matriz $A=A_{N\times N}$ é um quadrado latino de ordem $N$ se em cada linha e em cada coluna de $A$ aparecem todos os inteiros $1$, $2$, $\dots$, $N$ (ou seja, cada linha e cada coluna de $A$ é permutação dos inteiros $1$, $\dots$, $N$). Eis um exemplo de um quadrado latino de ordem $4$:
  \begin{equation*} \begin{bmatrix} 1 & 2 & 3 & 4 \\ 2 & 3 & 4 & 1 \\ 4 & 1 & 2 & 3 \\ 3 & 4 & 1 & 2 \\ \end{bmatrix} \end{equation*}
  Neste exercício, vamos supor que $N$ é no máximo NMAX.
  - Escreva uma função que recebe como parâmetros um inteiro $N$, um vetor $V$ com $N$ inteiros e verifica se em $V$ ocorrem todos os inteiros de $1$ a $N$.
  - Usando a função acima, verifique se uma dada matriz inteira $A=A_{N\times N}$ é um quadrado latino de ordem $N$.
- Problema 12 (Exercício 13 da lista de exercícios com funções III). Neste exercício, consideramos matrizes com no máximo MMAX linhas e no máximo NMAX colunas.
  - Escreva uma função que recebe como parâmetros uma matriz real $A=A_{M\times N}$ e uma posição $(i,j)$ da matriz, e calcula a média aritmética dos vizinhos de $(i,j)$, ou seja, a média entre $A_{i-1,j}$, $A_{i+1,j}$, $A_{i,j-1}$, e $A_{i,j+1}$. Desconsidere os "vizinhos" que "não pertencem à matriz" (por exemplo, os vizinhos de $(0,0)$ são somente $(0,1)$ e $(1,0)$).
  - Escreva uma função que recebe como parâmetro uma matriz real $A=A_{M\times N}$ e devolve uma matriz $A'$, onde $A_{i,j}'$ é a média aritmética dos vizinhos de $(i,j)$. Para isto, utilize a função do item anterior.
  - Escreva um programa que lê uma matriz real $A_{MxN}$ e um número inteiro $k$; utilizando a função do item anterior, o programa deve transformar a matriz $k$ vezes, imprimindo a matriz inicial e depois de cada transformação.
- Problema extra (Exercício 5 da lista de exercícios com funções III). Neste exercício, consideramos matrizes quadradas $N\times N$, com $N$ no máximo NMAX.
  - Escreva uma função que recebe como entrada um inteiro $N$, uma matriz inteira $A=A_{N\times N}$ e devolve três inteiros: $k$, $l$ e $c$ tais que $A_{l,c}=k$ e todos os elementos de $A$ são menores ou iguais a $k$ (isto é, $k$ é o maior valor presente em $A$).
  - Escreva um programa que, dado um inteiro $N$ e uma matriz quadrada de ordem $N$, cujos elementos são todos inteiros positivos, imprime uma tabela onde os elementos de $A$ são listados em ordem decrescente, acompanhados da posição de onde cada um dos elementos ocorre em $A$ (elementos repetidos podem ser listados em qualquer ordem). Utilize obrigatoriamente a função que você escreveu no item anterior.
    
    Por exemplo, com a matriz de entrada
    \begin{equation*} \begin{bmatrix} 3 & 7 & 1 \\ 1 & 2 & 8 \\ 5 & 3 & 4 \\ \end{bmatrix} \end{equation*}
    A saída poderia ser
    \begin{equation*} \begin{matrix} k & l & c \\ 8 & 1 & 2 \\ 7 & 0 & 1 \\ 5 & 2 & 0 \\ 4 & 2 & 2 \\ 3 & 0 & 0 \\ 3 & 2 & 1 \\ 2 & 1 & 1 \\ 1 & 0 & 2 \\ 1 & 1 & 0 \\ \end{matrix} \end{equation*}
[2020-06-09 Tue] Como sempre, a URL da aula será https://meet.google.com/hkd-fxan-zxg. Discutiremos o EP3 em mais detalhe nessa aula. Vamos também discutir os problemas da aula de [2020-06-04 Thu] que não pudemos discutir naquela aula por falta de tempo. Uma breve discussão sobre strings pode também ocorrer nessa aula.
[2020-06-11 Thu] Feriado (Decreto estadual)
[2020-06-16 Tue] Como sempre, a URL da aula será https://meet.google.com/hkd-fxan-zxg. Discutiremos strings, através dos seguintes problemas.
- Problema 13. Perfil de letras em texto.
  - Escreva uma função com protótipo
```
void calcule_perfil(char t[], int p[]); 
```
    que recebe um texto (um string) em $t$ e monta em $p$ o perfil de $t$: $p[0]$ deve ser o número de ocorrências de $'a'$ (ou $'A'$) em $t$, $p[1]$ deve ser o número de ocorrências de $'b'$ (ou $'B'$) em $t$, etc.
  - Escreva um programa lê uma palavra e determina uma letra que mais ocorre naquela palavra. Suponha que a palavra tenha no máximo NMAX caracteres.
  - (Variante) Faça o mesmo, supondo agora que a contagem deve ser feita em um texto de entrada.
- Problema 14. Ocorrência de uma palavra em um texto.
  - Escreva uma função com protótipo
```
int ocorre(char u[], char v[], int i); 
```
    que recebe dois strings $u$ e $v$, e um índice $i\geq0$, e devolve TRUE se $u$ aparece em $v$ a partir da posição $i$ e FALSE caso contrário.
  - Escreva um programa que recebe uma palavra na linha de comando e lê um texto da entrada padrão, e que imprime o número de ocorrências da palavra no texto. Use a função acima. Suponha que o texto tem no máximo TMAX caracteres.
- Problema 15. Comparação de strings.
  - Escreva uma função com protótipo
```
int strcmp(char u[], char v[]); 
```
    que recebe dois strings $u$ e $v$ e devolve $0$ se $u$ e $v$ são iguais, devolve um inteiro negativo se $u$ vem antes de $v$ na ordem alfabética e devolve um inteiro positivo se $u$ vem depois de $v$ na ordem alfabética.
  - Escreva um programa que leia uma sequência não vazia de nomes (com cada nome tendo no máximo NMAX caracteres), um nome por linha, e verifica se os nomes estão em ordem alfabética.
- Problema 16. Escreva uma função com protótipo
```
int indice(int v[], int N, int x);  
```
  que recebe um vetor $v$ de inteiros, com $N$ elementos ordenados em ordem crescente, e um inteiro $x$, e devolve $i$ tal que $v[i]=x$ se existir tal índice $i$. Se não existir tal $i$, a função deve devolver $-1$.
[2020-06-18 Thu] Como sempre, a URL da aula será https://meet.google.com/hkd-fxan-zxg. Continuaremos nossa discussão sobre busca e ordenação.
- Problema 16. Escreva uma função com protótipo
```
int indice(int v[], int N, int x);  
```
  que recebe um vetor $v$ de inteiros, com $N$ elementos ordenados em ordem crescente, e um inteiro $x$, e devolve $i$ tal que $v[i]=x$ se existir tal índice $i$. Se não existir tal $i$, a função deve devolver $-1$.
- Problema 17. Escreva uma função com protótipo
```
void ordene(int v[], int N);
```
  que recebe um vetor $v$ com $N$ números inteiros, e ordena os elementos de $v$ em ordem crescente.
  - Observação. Discutiremos algoritmos de ordenação brevemente. Esses são alguns ponteiros de interesse:
- Problema 18. Ordenação por colunas.
  - Escreva uma função de protótipo
```
void ordene_por_col(int A[][NMAX], int M, int N, int c);
```
    que recebe como parâmetros dois inteiros positivos $M$ e $N$, uma matriz de inteiros $A_{M\times N}$, o índice $c$ de uma coluna, e ordena as linhas de $A$ segundo a coluna $c$.
  - Dadas $0 < M\leq\verb|MMAX|$ datas em uma matriz $D_{M\times 3}$, onde a primeira coluna corresponde ao dia, a segunda ao mês e a terceira ao ano, colocar essas datas em ordem cronológica crescente, usando a função acima.
- Problema extra. Escreva um programa que recebe na linha de comando uma posição $(x, y)$ de um tabuleiro de xadrez e que lê um inteiro $k > 0$ e $k$ pares de inteiros que indicam as posicões de $k$ rainhas no tabuleiro. Seu programa deve dizer se a posição $(x, y)$ está sob ataque de uma das $k$ rainhas. Se estiver, seu programa deve dar a lista das rainhas que atacam $(x, y)$. Use uma matriz de caracteres para representar o tabuleiro. Use o caractere 'R' para representar uma rainha e '.' (ponto final) para representar uma posição vazia.
  - Escreva uma função de protótipo
```
void inicialize_tabuleiro(char tab[][MAX]);
```
    que inicializa a matriz tab com todas as posições vazias.
  - Escreva uma função de protótipo
```
void imprima_tabuleiro(char tab[][MAX]);
```
    que imprime o tabuleiro.
  - Escreva uma função de protótipo
```
int atacada(char tab[][MAX], int l, int c, int *l_R, int *c_R);
```
    que devolve TRUE se a posição $(l, c)$ está sendo atacada por alguma rainha no tabuleiro tab e devolve FALSE caso contrário. Se a posição estiver sendo atacada, então $(*l_R, *c_R)$ deve devolver a posição de uma rainha que ataca a posição $(l, c)$.
[2020-06-23 Tue] Como sempre, a URL da aula será https://meet.google.com/hkd-fxan-zxg. Inicialmente, vamos discutir o Problema 18, que acabou sobrando da aula de [2020-06-18 Thu]. Porém, o tópico principal dessa aula será alocação dinâmica de memória. Como preparação, veja o material em https://www.ime.usp.br/~pf/algoritmos/aulas/aloca.html (você pode ignorar a parte que fala sobre struct; de fato, aquela página contém mais material do que vamos conseguir discutir nessa aula). Faça os seguintes problemas, que envolvem alocação dinâmica de vetores e matrizes.
- Problema 19. Reversão de uma sequência de inteiros de comprimento arbitrário.
  - Escreva uma função de protótipo
```
int *leia_ints(int *N);
```
    que lê da entrada padrão um sequência de inteiros e devolve um vetor contendo esses inteiros. A função deve colocar em $*N$ o número de inteiros lidos. Não imponha nenhuma restrição no número de inteiros a serem lidos.
  - Dada uma sequência de inteiros de comprimento arbitrário, imprimir a sequência em ordem reversa.
- Problema 20. Ocorrência de uma palavra em um texto (variante do Problema 14).
  - Escreva um programa que recebe uma palavra na linha de comando e lê um texto da entrada padrão, e que imprime o número de ocorrências da palavra no texto. Não imponha nenhuma limitação no tamanho do texto.
- Problema 21. Suavização ("blurring") de imagens (variante do Problema 12).
  - Escreva um programa que lê uma imagem em formato PGM e cria uma versão suavizada dessa imagem. Não imponha restrições no tamanho da imagem. Veja o programa https://www.ime.usp.br/~yoshi/2020i/mac2166/sandbox/2020.06.09/PGM/suavize.c, discutido na aula de [2020-06-09 Tue].
- Problema 22. Ordenação de uma lista de nomes.
  - Escreva um programa que recebe uma lista de nomes, um nome por linha, e que imprime esses nomes em ordem alfabética. Não imponha nenhuma restrição no número de nomes, nem no comprimento de cada nome.
[2020-06-25 Thu] Problemas remanescentes da aula anterior. Discussão de eventuais dúvidas sobre o EP3
[2020-06-30 Tue] Semana de provas

Julho

[2020-07-02 Thu] Semana de provas
[2020-07-07 Tue] Como sempre, a URL da aula será https://meet.google.com/hkd-fxan-zxg. O tópico principal dessa aula será recursão. Como preparação, estude o material em https://www.ime.usp.br/~pf/algoritmos/aulas/recu.html. A seguir, faça os problemas abaixo, que envolvem ou podem ser resolvidos usando-se recursão. Para os Problemas 24, 25 e 26, essas transparências (páginas 5 e 6, páginas 11 e 12 e página 23) podem ajudar.
- Problema 23. Régua binária
  - Escreva uma função recursiva que imprima uma régua binária de ordem $N$. Nessa régua, o `traço' no ponto médio tem comprimento $N$, os traços nos pontos médios dos subintervalos superior e inferior têm comprimento $N−1$, e assim por diante. A figura abaixo mostra uma régua de ordem $4$.
```
. -
. --
. -
. ---
. -
. --
. -
. ----
. -
. --
. -
. ---
. -
. --
. -
```
- Problema 24. Contador binário
  - Escreva um programa que lista todas as cadeias de bits de comprimento $N$. Por exemplo, para $N=3$, seu programa deve imprimir
```
000
001
010
011
100
101
110
111
```
- Problema 25. Permutações
  - Escreva um programa que lista todas as permutações de $N$ objetos distintos. Por exemplo, para $1,2,3$, seu programa precisa imprimir a seguinte lista de permutações desses três inteiros distintos:
```
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
```
- Problema 26. Contador $R\text{-ário}$ (generalização do contador binário)
  - Escreva um programa que lista todas as cadeias de dígitos $R\text{-ários}$ de comprimento $N$. Por exemplo, para $R=2$, seu programa deve ser como no Problema 24 acima. Para $R=3$ e $N=2$, seu programa deve imprimir
```
00 
01
02
10 
11
12
20 
21
22
```
[2020-07-09 Thu] Como sempre, a URL da aula será https://meet.google.com/hkd-fxan-zxg. O tópico principal dessa aula será backtracking. Seguiremos essas transparências. Estudaremos o problema das rainhas e o Sudoku.
- MAC0122 Princípios de Desenvolvimento de Algoritmos
- Coursera. Cursos recomendados:

Página principal de MAC2166 (T3), 1o. semestre de 2020