Resenhas IME-USP 1995, Vol. 2, No. 2, 209-217.
An Algorithm to Classify 3-Manifolds?
Sóstenes L. Lins
Department of Mathematics
Federal University of Pernambuco
Recife, PE
Brazil
E-mail address: sostenes@dmat.ufpe.br
Abstract
Combinatorial topology makes unlimited use of refinements. These refinements
translate into an unlimited amount of data to describe objects like
3-manifolds. As a result, procedures to treat the homeomorphism problem, by
combinatorial means, become unfeasible.
In this article we describe a finite algorithm which attains a combinatorial
classification of 3-gems (tridimensional manifolds encoded by graphs), see
[S.L. Lins, Gems, Computers and Attractors for 3-Manifolds, Number 5 in
Knots and Everything, World Scientific, 1995] or Chapter 13 of
[L.H. Kauffman and S.L. Lins, Temperley-Lieb Recoupling Theory and Invariants
of 3-Manifolds, Number 134 in Annals of Mathematical Studies, Princeton
University Press, 1994]. Up to the level studied (3-gems of 30 vertices), the
combinatorial classification coincides with the topological one. A general
question arises as at what level the combinatorial classes no longer coincides
with the classes of homeomorphisms. The hope that this coincidence can always
hold enable us to enunciate a conjecture that would computationally classify
closed 3-manifolds.
The central point in our approach is that the type of refinements in 3-gems
that we permit (the U-move) are only applied in conjunction with some
horizontal moves (the TS-moves that do not increase the size of the
objects) and by others (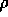 -moves) which
decrease its size in such a way that the final 3-gem has no more vertices than
the original one.
-moves) which
decrease its size in such a way that the final 3-gem has no more vertices than
the original one.
Back to Table of Contents
Last modified: Tue Oct 31 17:51:12 GMT 1995
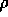 -moves) which
decrease its size in such a way that the final 3-gem has no more vertices than
the original one.
-moves) which
decrease its size in such a way that the final 3-gem has no more vertices than
the original one.