
Esta página contém o material didático dos assuntos a serem estudados na semana.
Cada novo assunto tem exercícios recomendados, que serão discutidos pelos professores nos plantões online da disciplina.
É muito importante que os alunos estudem os materiais e exercícios recomendados para a semana antes do plantão online da sua turma.
O assunto da semana é:
O assunto da semana anterior foi:
Para consultar o material didático das aulas dadas nas semanas anteriores, acesse o Guia de Estudos Completo de MAC2166.
n > 0 valores inteiros, em uma lista
L, e um inteiro x, testa se
x pertence à lista.
Solução 1:
Solução por busca exaustiva percorrendo a lista (busca sequencial).
def pertence(x, L):
n = len(L)
i = 0
while i < n:
if L[i] == x:
return True
i += 1
return False
Solução 2:
Essa solução
adiciona na posição seguinte a do último elemento
o valor de x, conseguindo com isso a
simplificação do laço que passa agora a realizar
uma única comparação para cada iteração.
Essa técnica de busca é
conhecida como busca com sentinela.
# busca com sentinela
def pertence(x, L):
n = len(L)
i = 0
L.append(x) #adiciona x no final da lista
while L[i] != x:
i += 1
L.pop() #remove x do final da lista
if i == n:
return False
else:
return True
O algoritmo usado nas duas implementações da função pertence(x,L) acima é chamado de Busca Linear (ou Busca Sequencial). Observe que, nesse algoritmo, toda a lista precisa ser varrida quando o x procurado não está em L.
Mas é possível deixar esse algoritmo mais eficiente quando os elementos da lista na qual se quer buscar um valor estão ordenados, detectando que um elemento não está na lista ordenada mesmo antes de chegar ao seu final. Para isso, basta percorrer os elementos da lista em ordem crescente e encerrar o algoritmo quando x ou um valor maior do que ele for encontrado. Também é possível percorrer os elementos da lista em ordem descrescente; nesse caso, deve-se encerrar o algoritmo quando x ou um valor menor do que for encontrado.
n > 0 valores inteiros ordenados, em uma lista
L, e um inteiro x, testa se
x pertence à lista.
Quando a lista está ordenada, a busca pode ser ainda mais eficiente que a descrita acima. Para isso, usamos uma estratégia parecida com a forma como buscamos palavras em um dicionário ou nomes em um catálogo de telefones ou endereços em papel. Nesse caso, ao invés de testar um elemento de cada vez sequencialmente, podemos aplicar o seguinte algoritmo:
Observe que nesse algoritmo, a cada vez que executamos os passos 3 ou 4, metade da lista é eliminada da busca. É por isso que o algoritmo é chamado de Busca Binária.
Para "enxergar" melhor quão mais eficiente a Busca Binária é em relação à Busca Sequencial, considere o seguinte exemplo: procuramos um dado x em uma sequência ordenada com 512 elementos, mas x não está nesta sequência. Antes de indicar que x não está na sequência, o algoritmo de Busca Sequencial precisa testar todos os 512 elementos da sequência. No caso da Busca Binária, o primeiro teste elimina 256 elementos, o segundo 128, o terceiro 64, e depois 32, 16, 8, 4, 2, até que a lista contenha apenas 1 elemento. Dessa forma, ao invés de 512, apenas 9 elementos (ou log(len(L))) precisam ser testados.
Escreva uma função que implemente o algoritmo da Busca Binária. A sua função deve receber como parâmetro uma lista ordenada e um número real x e devolver a posição em que x ocorre na lista ou None caso x não esteja na lista.
Escreva uma função recursiva que implemente o algoritmo da Busca Binária. A sua função deve receber como parâmetro uma lista ordenada e um número real x e devolver a posição em que x ocorre na lista ou None caso x não esteja na lista.
L com n > 0 números inteiros no intervalo de 0 a 255
(isto é, 0 <= L[i] <= 255 para i = 0,.., n-1),
faça uma função para ordenar os seus elementos em ordem crescente.
Solução 1:
Explorando o fato de que os valores estão em um intervalo limitado de 0 a 255, podemo usar o algoritmo de ordenação do Counting Sort. Para isso vamos usar uma lista de contadores para cada valor de 0 a 255. Portanto, o algoritmo necessita de memória auxiliar.
def ordenacao_por_contagem(L):
n = len(L)
C = [0]*256 #Lista de contadores
for i in range(0,n):
C[L[i]] += 1
#Agora C[k] contém o número de elementos iguais a k.
i = 0
for k in range(0,256):
for c in range(0,C[k]):
L[i] = k
i += 1
Solução 1:
Dividimos ao meio a lista e ordenamos as duas metades via duas chamadas recursivas. A ordenação final é então obtida via intercalação dos valores das duas metades ordenadas.
def mergeSortAux(L, inic, fim):
if fim - inic + 1 <= 1:
return
m = (inic + fim)//2
mergeSortAux(L, inic, m)
mergeSortAux(L, m+1, fim)
A = []
i = inic
j = m+1
while i <= m or j <= fim:
if i > m:
A.append(L[j])
j += 1
elif j > fim:
A.append(L[i])
i += 1
elif L[i] < L[j]:
A.append(L[i])
i += 1
else:
A.append(L[j])
j += 1
for k in range(inic, fim+1):
L[k] = A[k-inic]
def mergeSort(L):
n = len(L)
mergeSortAux(L, 0, n-1)
Exemplo de função principal que chama as
funções anteriores.
def main():
L = [6,3,9,2,7,1,0,4,8,5]
ordenacao_insercao(L)
for i in range(0,n):
print(L[i], end=" ")
print()
x = int(input("Digite x: "))
if pertence(x, L):
print("Sim")
else:
print("Não")
main()
Veja a videoaula do prof. Fabio Kon (IME-USP) sobre Recursão:
Uma função é dita recursiva quando dentro dela é feita uma ou mais chamadas a ela mesma.
A ideia é dividir um problema original um subproblemas menores de mesma natureza (divisão) e depois combinar as soluções obtidas para gerar a solução do problema original de tamanho maior (conquista). Os subproblemas são resolvidos recursivamente do mesmo modo em função de instâncias menores, até se tornarem problemas triviais que são resolvidos de forma direta, interrompendo a recursão.
Solução 1:
Solução não recursiva.
def fatorial(n):
fat = 1
while n > 1:
fat *= n
n -= 1
return fat
Solução 2:
Solução recursiva: n! = n.(n-1)!

def fatorial(n):
if n == 0: #Caso trivial
return 1 #Solução direta
else:
return n*fatorial(n-1) #Chamada recursiva

Exemplo da sequência:
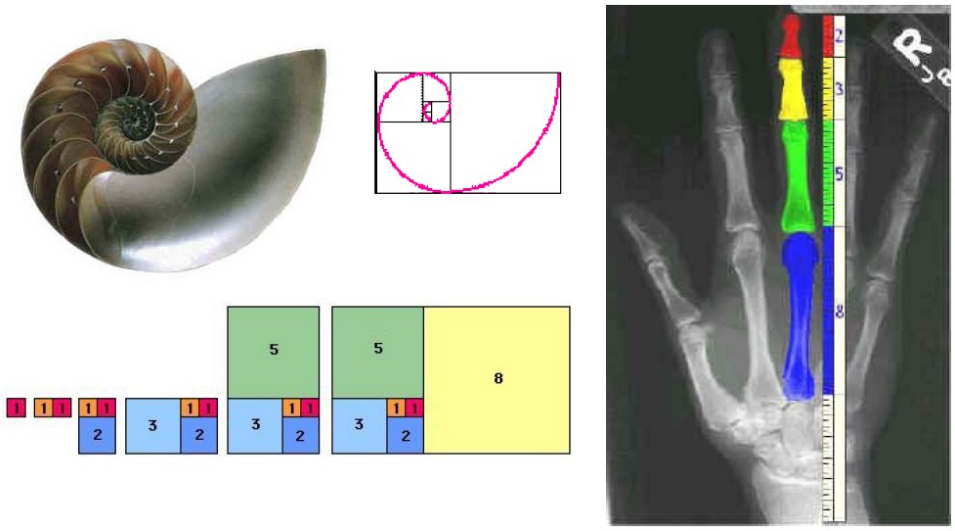
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...A ocorrência da sucessão de Fibonacci na natureza é tão frequente que é difícil acreditar que seja acidental (ex: flores, conchas, mão humana).
Solução 1:
Versão recursiva:
def fibo(n):
if n <= 1:
return n
else:
return fibo(n-1) + fibo(n-2)
Solução 2:
Versão não recursiva:
def fibo(n):
f0 = 0
f1 = 1
for k in range(1,n+1):
f2 = f0 + f1
f0 = f1
f1 = f2
return f0
Análise de eficiência das funções
Fibonacci calculando o número de operações
de soma S(n) realizadas:

Neste caso não faz sentido utilizar a versão recursiva.
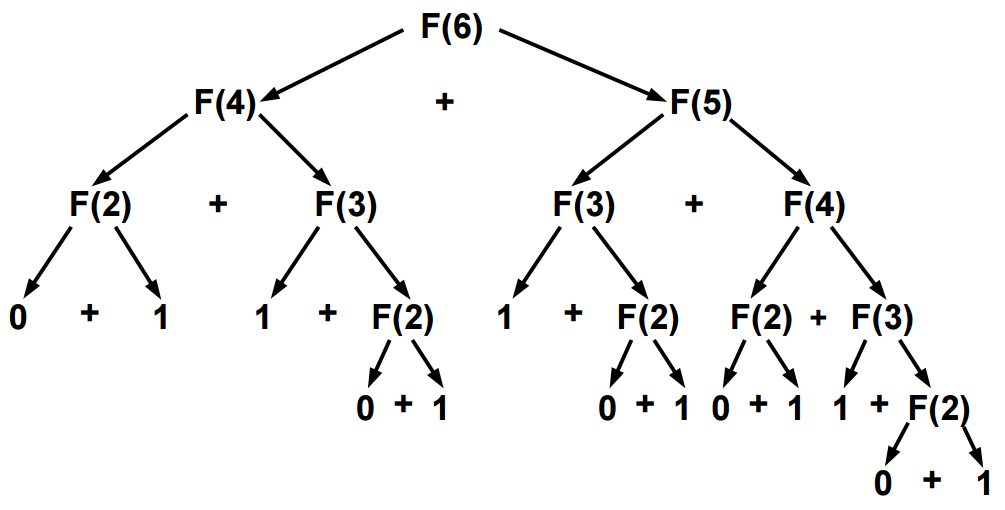
Árvore de Recorrência:
A solução recursiva é ineficiente, pois recalcula várias vezes a solução para valores intermediários:
Por exemplo, para F(6)=fibo(6) = 8, temos 2xF(4), 3xF(3), 5xF(2).
potencia(x, n), que calcule
x elevado a n, sendo x um número real
e n um inteiro positivo.
Problema 4:
Faça uma função recursiva que recebe uma lista e que devolve o maior valor dela.
Problema 5:
Faça uma função recursiva que recebe uma lista
e que devolve uma segunda lista de mesmo comprimento, mas
com os elementos em ordem reversa.
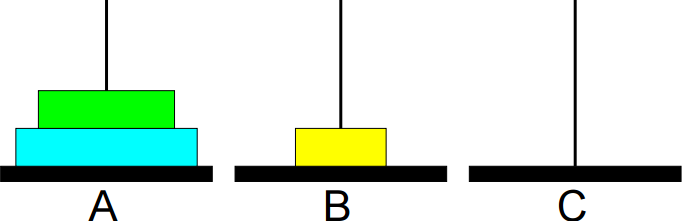
Problema 6: Torre de Hanoi
São dados um conjunto de n discos com diferentes tamanhos e
três bases A, B e C.
O problema consiste em imprimir os passos necessários para
transferir os discos da base A para a base B, usando a base C
como auxiliar, nunca colocando discos maiores sobre menores.
Exemplo:

1º passo: Mover de A para B.
2º passo: Mover de A para C.
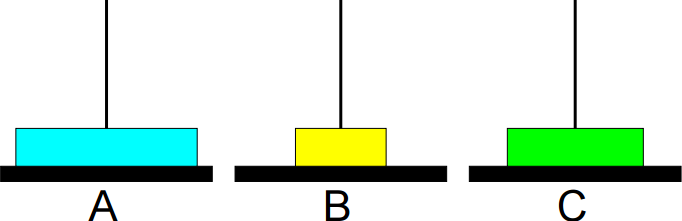
3º passo: Mover de B para C.
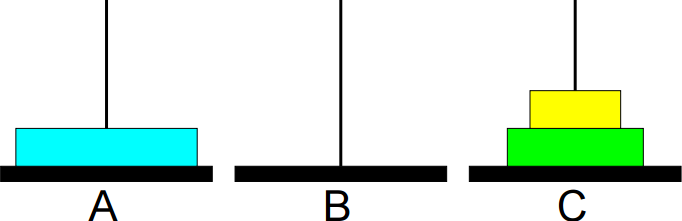
4º passo: Mover de A para B.
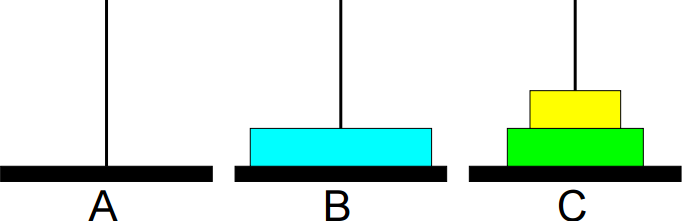
5º passo: Mover de C para A.

6º passo: Mover de C para B.
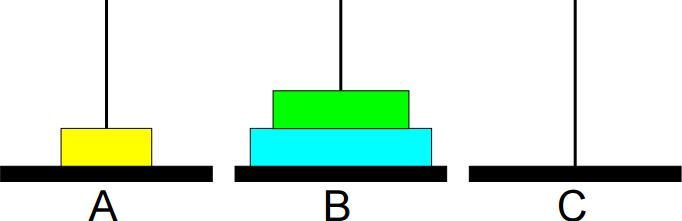
7º passo: Mover de A para B.
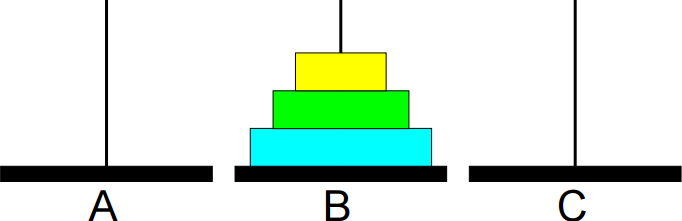
Animação da sequência completa de movimentos:
