Veja também o vídeo abaixo, intitulado "O que é ciência da computação", do prof. Fabio Kon (IME-USP).
Veja também o vídeo abaixo, intitulado "O que é Software Livre?", do Nelson Lago (IME-USP).
print())input())str e intint()whileO vídeo abaixo mostra como fazer a instalação do python e IDLE no Windows.
O vídeo abaixo mostra como fazer a instalação do python e IDLE no Linux (ubuntu)
via linha de comando no terminal, usando apt-get.
O IDLE 3 pode também ser instalado no Ubuntu procurando por IDLE3 no Synaptic Package Manager do Ubuntu, tal como mostrado abaixo.

Após instalar o IDLE3, você pode então abrir o Python Shell, clicando no ícone indicado abaixo.
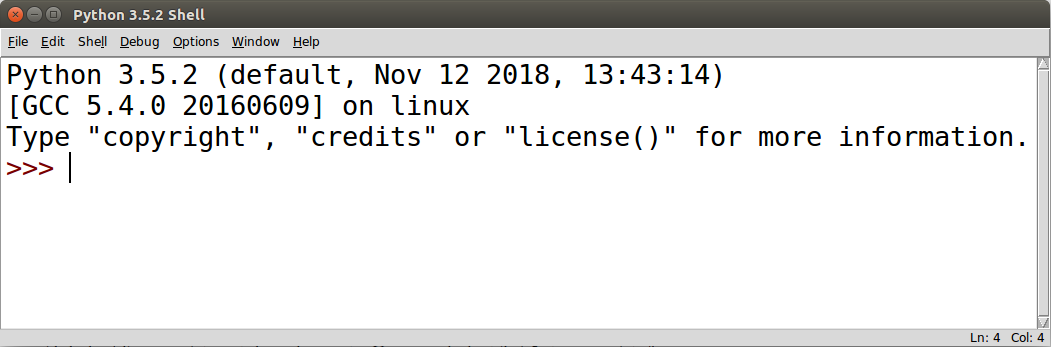
Ao abrir o Python Shell, será exibida uma janela
com o cursor piscando em frente ao prompt >>>,
indicando que o sistema está pronto para receber comandos.
Um comando é uma unidade de código que o interpretador do Python
pode executar. Neste curso, estamos usando a versão 3 do Python.
Por exemplo, podemos usar o Python Shell para fazer contas, tal como em uma calculadora.
Veja o exemplo abaixo digitado no prompt (>>>) do Python shell:
>>> 2 + 3 * 620>>> (2+3)*630
Observe que a multiplicação (representada pelo símbolo *) tem precedência sobre a adição. Logo, o uso de parênteses se faz necessário quando queremos primeiramente calcular a soma.
A tabela abaixo apresenta a lista de operadores aritméticos do Python.
| Operador | Descrição | Exemplo | Avalia para |
|---|---|---|---|
| + | Adição | 7 + 3 | 10 |
| - | Subtração | 7 - 3 | 4 |
| * | Multiplicação | 7 * 3 | 21 |
| / | Divisão (Real) | 7 / 3 | 2.3333333333333335 |
| // | Divisão (Inteiro) | 7 // 3 | 2 |
| % | Módulo (resto da divisão) | 7 % 3 | 1 |
Veja o vídeo abaixo, intitulado "Primeiras linhas em Python", do prof. Fabio Kon (IME-USP).
Porém, tome cuidado, pois nesse vídeo está sendo usada a versão 2 do Python e não o Python 3, o que gera uma diferença na saída do operador de divisão.
Uma variável é um nome que se refere a um valor armazenado na memória do computador. Um comando de atribuição (=) cria uma nova variável e lhe dá um valor.
Um comando de atribuição tem a seguinte forma:
variável = expressãoSignificado:
Variáveis são usadas para guardarmos valores que serão usados mais tarde no programa.
Por exemplo, variáveis podem ser usadas como parte de futuras expressões matemáticas, indicando que seus valores serão usados como operandos dos operadores.
Note, porém, que uma variável não pode ser usada em uma expressão antes de sua criação.
A qualquer momento podemos imprimir/exibir o valor de uma variável
usando o comando print, tal como indicado no exemplo abaixo:
>>> a = 2 + 3 * 6>>> print(a)20>>> b = a - 5>>> print(b)15
Nomes de variáveis devem obedecer à seguinte regra de formação.
Os nomes das variáveis devem começar por uma letra
ou o símbolo '_' (underscore)
e depois conter somente letras, números ou underscore.
Atenção, maiúscula é diferente de minúscula. Assim maior e Maior são duas variáveis diferentes. Abaixo são apresentados alguns exemplos de nomes de
variáveis válidos digitados no prompt (>>>) do Python shell.
>>> valor_bruto = 1000>>> _valor = 75>>> bola8 = 50>>> DocumentoDeIdentidade = 123456789Abaixo é apresentado um exemplo de nome de variável inválido (por iniciar com um número) digitado no prompt (>>>) do Python shell. Observe a mensagem de erro indicando que o comando não pôde ser processado pelo interpretador.
>>> 8bola = 50SyntaxError: invalid syntax
a = a + b do Python
não implica que b = 0.
Isto é, o comando em questão não é uma equação matemática, logo você não deve subtrair 'a' dos dois lados para tirar conclusões.
O valor contido no espaço de memória de uma variável
pode variar com o tempo, não sendo um valor fixo
durante todo tempo de execução de um programa.
Desse modo, comandos como a=a-4
são perfeitamente aceitáveis.
No exemplo abaixo, a variável a recebe inicialmente o valor 14. Na sequência, o comando a=a-4 é executado, sendo sua expressão do lado direito a-4 então avaliada como 14-4 e, consequentemente, resultando em 10. Esse novo valor 10 passa então a ser armazenado na
variável a, sobrescrevendo seu valor anterior 14 que é perdido.
>>> a = 14>>> print(a)14>>> a = a - 4>>> print(a)10
Podemos imprimir os valores de múltiplas variáveis em um único comando print, passando as variáveis separadas por vírgulas.
>>> a = 3>>> b = 2>>> print(a, b)3 2
Um problema recorrente em computação é o de
trocar/inverter o valor entre duas variáveis. Isso será
especialmente útil para a ordenação de dados em
aulas futuras.
Por exemplo, se a = 3 e b = 2 para trocar
seu valores poderíamos pensar em usar o seguinte código:
>>> a = b>>> b = a>>> print(a, b)2 2
No entanto, o código acima não funciona, pois o primeiro
comando de atribuição sobrescreverá o valor 3
armazenado na variável a que será perdido.
De modo que, no final teremos o valor 2 nas duas variáveis
a e b.
Uma solução correta pode ser encontrada no código abaixo.
A ideia é utilizar uma terceira variável auxiliar
para guardar uma cópia de backup do valor original 3 da variável a, antes de copiar em a o valor 2 contido em b.
>>> t = a>>> a = b>>> b = t>>> print(a, b)2 3
O Python possui vários atalhos, logo para trocar o valor entre
variáveis podemos usar também o seguinte código abaixo.
Porém, note que, a solução abaixo é
específica para códigos em Python.
>>> a,b = b,a>>> print(a, b)2 3
Em Python, podemos usar variáveis também para armazenar
e processar textos.
Na programação de computadores,
uma cadeia de caracteres, mais conhecida como string,
é uma sequência de letras e símbolos
(na qual os símbolos podem ser espaços em branco, dígitos e vários outros como pontos de exclamação e interrogação, símbolos matemáticos, etc),
geralmente utilizada para representar palavras, frases ou textos de um programa.
Em um programa Python, strings podem ser especificadas
como textos delimitados por aspas duplas ou simples.
Somando duas strings obtemos uma nova string
resultante da concatenação das duas primeiras.
Veja o exemplo abaixo digitado no prompt (>>>) do Python shell:
>>> a = "Paulo">>> b = "Miranda">>> c = a + b>>> print(c)PauloMirandaDado que é possível somar duas strings, poderíamos pensar que é possível também somar uma string com um número inteiro, mas esta não é uma operação definida no Python. Como resultado temos a mensagem de erro indicada no exemplo abaixo.
>>> "Paulo" + 5Traceback (most recent call last): File "", line 1, in "Paulo" + 5TypeError: Can't convert 'int' object to str implicitlyPor outro lado, curiosamente, podemos multiplicar uma string por um inteiro em Python. O resultado é a criação de uma nova string contendo o texto repetido o número de vezes indicado.
>>> "Bla"*10'BlaBlaBlaBlaBlaBlaBlaBlaBlaBla'
Dado que em Python podemos ter diferentes tipos de dados armazenados em uma
variável, como descobrir o tipo de dado armazenado em uma variável
preexistente se torna uma pergunta pertinente.
Para saber o tipo de dado armazenado em uma variável podemos usar o comando type:
>>> a = 37>>> type(a)<class 'int'>>>> a = "Paulo">>> type(a)<class 'str'>
Textos são representados por objetos da classe str (string),
enquanto inteiros são representados por objetos da classe int .
Para mais informações e exemplos sobre os tipos de dados em Python, veja o vídeo abaixo, intitulado "Valores e tipos em Python", do prof. Fabio Kon (IME-USP).
Dado que nos exemplos acima estamos usando as aspas duplas
como delimitadores de string,
uma pergunta oportuna é, portanto, a seguinte:
como podemos inserir o caractere de aspas dupla (") como parte do texto de uma string?
Uma resposta é considerar aspas simples como delimitadores sempre que queremos inserir aspas duplas dentro do texto e vice-versa.
Veja os exemplos abaixo digitados no prompt (>>>) do Python shell:
>>> a = 'Camões escreveu "Os Lusíadas" no século XVI.'>>> print(a)Camões escreveu "Os Lusíadas" no século XVI.>>> b = "Esperamos o 'feedback' da professora.">>> print(b)Esperamos o 'feedback' da professora.Outra solução é considerar sequências de escape.
Os caracteres ou sequências de escape são usadas para conseguir imprimir na tela caracteres especiais ou símbolos, que são impossíveis de obter normalmente. Exemplos comuns são as aspas simples ou duplas, que por já estarem sendo usadas como delimitadores da string geram as dificuldades vistas anteriormente para serem inseridas como partes integrantes do conteúdo da string. Outros exemplos são os de caracteres que não possuem um símbolo gráfico correspondente, tais como o caracter de pula linha e o de tabulação.
Esses caracteres especiais são especificados por meio de combinações de outros caracteres, denominadas sequências de escape, que sempre iniciam com uma barra invertida (\). O próprio caractere de barra invertida se torna um
caractere especial por ser reservado para indicar o início de
uma nova sequência de escape.
A tabela abaixo apresenta os caracteres de escape do Python:
| Sequência de escape | Descrição |
|---|---|
| \\ | Barra invertida (Backslash). Insere uma barra invertida. |
| \' | Aspas simples (Single quote). Insere uma aspas simples. |
| \" | Aspas duplas (Double quote). Insere uma aspas duplas. |
| \n | Nova linha (NewLine). Move o cursor para o início da próxima linha. |
| \t | Tabulação horizontal (Horizontal tab). Move o cursor uma tabulação para frente. |
Experimente digitar no prompt (>>>) do Python shell os comandos abaixo:
>>> a = "Camões escreveu \"Os Lusíadas\" no século XVI.">>> print(a)Camões escreveu "Os Lusíadas" no século XVI.>>> b = "Primeira linha.\nSegunda linha.">>> print(b)Primeira linha.Segunda linha.>>> c = "\tCom tabulação.\nSem tabulação.">>> print(c) Com tabulação.Sem tabulação.>>> d = "Barra invertida: \\">>> print(d)Barra invertida: \>>> e = "\\\\\\" #Imprime três barras invertidas.>>> print(e)\\\
O texto em vermelho (#Imprime três barras invertidas.) usado no exemplo acima é um comentário, tal como explicado abaixo.
#,
tudo que estiver depois do # e na mesma linha será ignorado pelo interpretador.
A alternativa consiste em salvar o código em um arquivo (script) e então invocar o interpretador para executá-lo. Por convenção, os scripts no Python são arquivos texto com nomes que terminam com a extensão .py. Vamos fazer nosso primeiro programa em Python no modo script. Na janela do Python Shell, você deve clicar em "File" e depois em "New File". Vai ser aberto um editor de texto, conforme ilustrado abaixo.
Digite então o exemplo do código abaixo e salve o arquivo, por exemplo, como "programa.py".
idade = input("Digite sua idade: ")
print("Nossa, parece que você tem", idade*2, "anos.")
O programa acima solicita que o usuário digite sua idade. Na sequência,
a intenção do programa é imprimir uma mensagem "trollando" o
usuário, dizendo que ele aparenta ter o dobro da idade.
Para a leitura dos dados, vamos introduzir um novo comando, o comando input().
O comando input(), primeiramente imprime a string passada como
parâmetro "Digite sua idade: " e, em seguida, ativa o modo de digitação,
isto é, o cursor vai ficar piscando no Python Shell/terminal esperando a digitação (entrada de dados), seguida de ENTER.
Para invocar o interpretador Python para executar o programa acima criado no modo script,
você deve clicar em "Run" e depois em "Run Module".

Abaixo é mostrado um exemplo de execução do programa, assumindo que o usuário possui 39 anos de idade. Ou seja, o texto em preto foi digitado pelo usuário.
Digite sua idade: 39Nossa, parece que você tem 3939 anos.Aparentemente algo deu errado, visto que o programa imprimiu que o usuário aparenta ter três mil e novecentos e trinta e nove anos. Ou seja, mais que a idade ao morrer de Matusalém.
O problema ocorreu porque a devolução do valor digitado pelo comando input() sempre se dá na forma de uma string
e, como vimos anteriormente, a multiplicação de
uma string por um inteiro causa a sua repetição (isto é,
"39"*2 gera a string "3939").
Portanto, precisamos converter a string lida para um inteiro antes de calcular o
produto. Para isso, podemos usar o comando int() que
converte a string passada como parâmetro para o inteiro correspondente,
tal como indicado no exemplo abaixo digitado no prompt (>>>) do Python shell:
>>> a = "39">>> type(a)<class 'str'>>>> a = int(a)>>> type(a)<class 'int'>>>> print(a)39Uma versão corrigida do programa é apresentada abaixo.
idade = input("Digite sua idade: ")
idade = int(idade)
print("Nossa, parece que você tem", idade*2, "anos.")
A execução da nova versão do programa com valor de entrada 39, agora apresenta o resultado esperado:
Digite sua idade: 39Nossa, parece que você tem 78 anos.
Esse programa pode ser escrito de modo mais compacto
usando os comandos int() e input()
de modo aninhado, isto é, como int(input()).
idade = int(input("Digite sua idade: "))
print("Nossa, parece que você tem", idade*2, "anos.")
Para outros exemplos de programas com o comando input(), veja também o vídeo abaixo, intitulado "Entrada de dados", do prof. Fabio Kon (IME-USP).
Veja também o vídeo abaixo, intitulado "Executando programas em python", do Nelson Lago (IME-USP).
No Python, é possível também comparar valores
utilizando operadores relacionais.
Operadores relacionais serão especialmente úteis
na construção de comandos condicionais e
comandos de repetição.
Operadores relacionais executam ações com dois operandos,
produzindo como resultado verdadeiro ou falso (True ou False).
A tabela abaixo apresenta a relação dos operadores relacionais do Python.
| Operador | Descrição | Exemplo | Avalia para |
|---|---|---|---|
| == | igual a | 5 == 5 | True |
| != | diferente de | 8 != 5 | True |
| > | Maior que | 3 > 10 | False |
| < | Menor que | 5 < 8 | True |
| >= | Maior ou igual a | 5 >= 10 | False |
| <= | Menor ou igual a | 5 <= 5 | True |
Por exemplo, experimente digitar no prompt (>>>) do Python shell os comandos abaixo:
>>> 8 > 5True>>> 3 < 2False>>> x = 7>>> x < 9True>>> x == 7True>>> x != 7False
O resultado de operadores relacionais podem ser atribuídos a
variáveis e podemos usar o comando type
para descobrir o tipo de dado resultante.
>>> a = 2 < 8>>> type(a)<class 'bool'>>>> print(a)True
Os valores True e False devolvidos por operadores
relacionais são da classe bool (boolean em
homenagem ao matemático George Boole).
Dado que o operador de adição pode também
ser empregado com strings, conforme visto anteriormente,
será que operadores relacionais também se aplicam a strings?
Abaixo são apresentados alguns testes realizados
no prompt (>>>) do Python shell:
>>> "Corinthians" == "Campeão"False>>> "São Paulo" > "Corinthians"True
Deixando de lado a brincadeira com os corintianos,
observamos que, de fato, os operadores relacionais podem ser usados com strings.
O operador de igualdade (==)
somente devolverá o valor True se
as duas strings forem idênticas.
Lembre-se que Python diferencia minúsculas de maiúsculas.
Portanto, a comparação "paulo" == "PAULO" devolverá False.
Comparações do tipo "maior que" e "menor que"
comparam as strings levando em conta a ordem lexicográfica
(ordem alfabética no caso da comparação entre letras minúsculas
com minúsculas e maiúsculas com maiúsculas).
Portanto, "São Paulo" > "Corinthians" é True não porque o primeiro time possui mais títulos, mas porque "S" sucede "C" na ordem do alfabeto.
A seguir, veremos nosso primeiro comando de repetição. Dentro da lógica de programação, comandos de repetição (Laços ou Loops) são estruturas que nos permitem executar mais de uma vez o mesmo comando ou conjunto de comandos, de acordo com uma condição de controle.

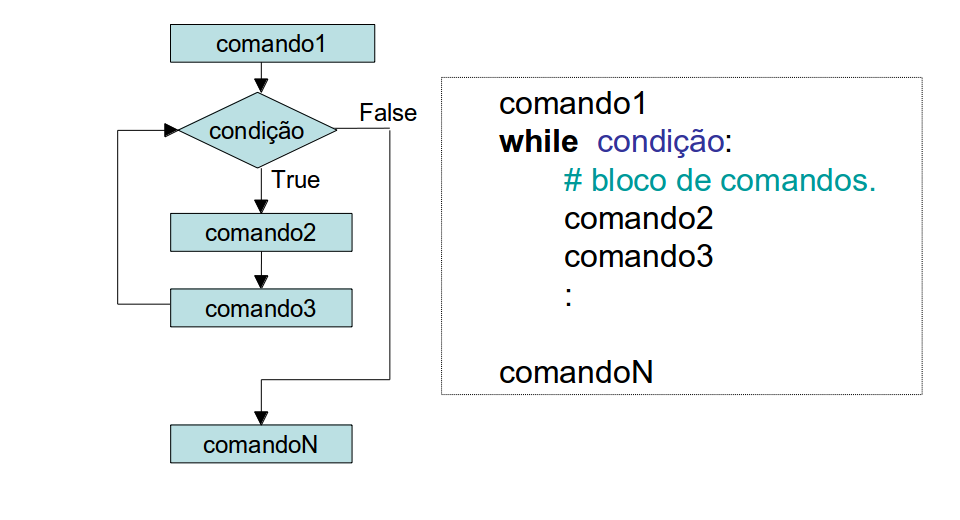
O comando de repetição while ("enquanto")
é a mais difundida estrutura de repetição.
Nesta estrutura, a condição é primeiramente verificada, e se for verdadeira o bloco é executado. No final da execução do bloco a condição é novamente testada.
Entende-se por condição qualquer comando Python que produza
como saída verdadeiro (True) ou falso (False).
Até o presente momento, os únicos comandos vistos
com tal propriedade foram os operadores relacionais.
O fluxograma de execução do comando while
é exibido abaixo:
1 + 2 + 3 + ... + n).
Uma primeira solução usando o comando while
é apresentada abaixo.
soma = 0
i = 1
while i <= n:
soma = soma + i
i = i + 1
print("A soma de 1 a",n,"é",soma)
A solução anterior é uma
solução ingênua.
Observe que a soma 1 + 2 + 3 + ... + n corresponde a soma dos termos de uma PA de razão 1.
Logo, uma solução mais eficiente consiste em aplicar
diretamente a fórmula da soma dos termos da PA.
n = int(input("Digite n: "))
soma = ((1+n)*n)//2
print("A soma de 1 a",n,"é",soma)
12 17 4 -6 8 0
o seu programa deve escrever o número 35.
Uma primeira solução é apresentada abaixo.
num = 1
soma = 0
while num != 0:
num = int(input("Digite um inteiro: "))
soma = soma + num
print("A soma é",soma)
Outra versão:
num = int(input("Digite um inteiro: "))
soma = 0
while num != 0:
soma = soma + num
num = int(input("Digite um inteiro: "))
print("A soma é",soma)
Uma primeira solução usando o comando while
é apresentada abaixo.
n = int(input("Digite o valor de n: "))
k = int(input("Digite o valor de k: "))
pot = 1
i = 0
while i < k:
pot = pot*n
i = i + 1
print("A potência é",pot)
No Python, podemos também usar o operador de
exponenciação **:
n = int(input("Digite o valor de n: "))
k = int(input("Digite o valor de k: "))
pot = n**k
print("A potência é",pot)
n! = n*(n-1)*(n-2)*...*1Uma primeira solução usando o comando
while
é apresentada abaixo.
n = int(input("Digite o valor de n: "))
fat = 1
i = 2
while i <= n:
fat = fat*i
i = i + 1
print("Fatorial de",n,"é",fat)
No Python, podemos também usar
funções matemáticas prontas do
módulo math do Python.
Para isso, devemos primeiramente importar o módulo math,
usando o comando import math, e depois chamar a função math.factorial().
import math
n = int(input("Digite o valor de n: "))
fat = math.factorial(n)
print("Fatorial de",n,"é",fat)
//%a,b,c e d, tal que a = 1.3432, b = 342.02,
c = 3000.8023 e d = 20900.978234,
faça um programa que exibe os 4 valores com duas casas de precisão após a vírgula, e na forma de uma tabela, conforme o
exemplo abaixo:
| a: 1.34 | b: 342.02 | | c: 3000.80 | d: 20900.98 |
Solução:
print("| a: %8.2f | b: %8.2f |"%(a,b))
print("| c: %8.2f | d: %8.2f |"%(c,d))
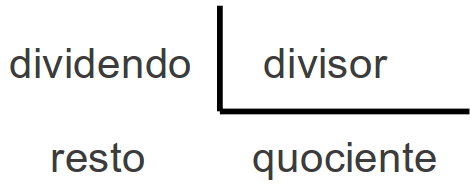
| Operador | Nome | Explicação | Exemplos |
|---|---|---|---|
| // | Divisão Inteira | Retorna a parte inteira do quociente | 7 // 2 retorna 3 |
| % | Módulo | Retorna o resto da divisão | 7 % 2 retorna 1 |
 |
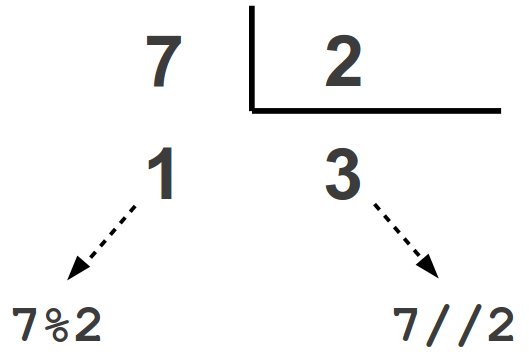 |
x é par ou ímpar,
devemos verificar se x é divisível ou não por 2.
Veja abaixo alguns exemplos de comandos digitados no prompt (>>>) do Python shell:
>>> x = 5>>> x % 2 == 0 #Testa se x é par.False>>> x % 2 == 1 #Testa se x é ímpar.True>>> x = 6>>> x % 2 == 0 #Testa se x é par.True>>> x % 2 == 1 #Testa se x é ímpar.False
O dígito menos significativo de um inteiro contido em uma
variável x pode ser obtido tomando o seu resto da divisão por 10, isto é, r = x % 10. Uma vez processado esse dígito em r, podemos então
removê-lo de x usando sua divisão inteira por 10, isto é, x = x // 10. Repetindo o processo, podemos
então acessar os demais dígitos, do menos significativo
em direção ao mais significativo.
Veja o exemplo abaixo digitado no prompt (>>>) do Python shell:
>>> x = 6583>>> x % 103>>> x = x // 10>>> x % 108>>> x = x // 10>>> x % 105>>> x = x // 10>>> x % 106
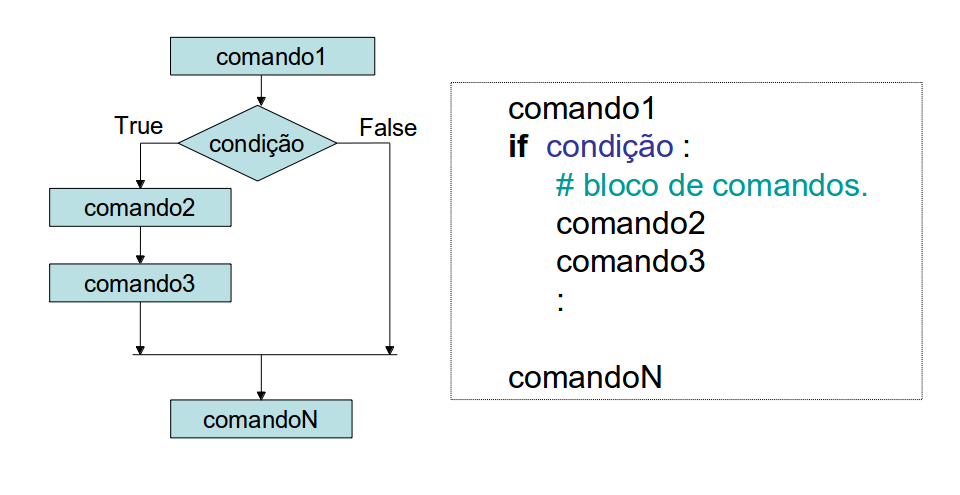
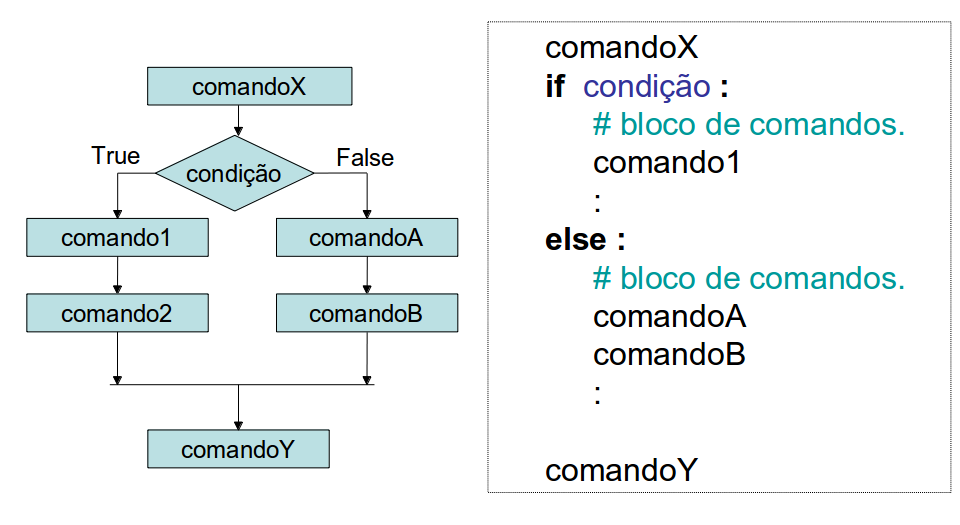
Permite a escolha de um grupo de comandos
(bloco de comandos) quando uma determinada
condição lógica é satisfeita.
6 -2 7 0 -5 8 4
o seu programa deve escrever o
número 4 para o número de pares.
Uma primeira solução é apresentada abaixo.
n = int(input("Digite o tam da seq: "))
conta_par = 0 # Contador de números pares encontrados.
i = 1
while i <= n:
num = int(input("Digite um num da seq: "))
if num % 2 == 0: # Testa se num é par.
conta_par = conta_par + 1
i = i + 1
print("Quant. pares =", conta_par)
# Fim do programa.
Uma segunda versão que decrementa o próprio valor em n
para controlar o laço.
n = int(input("Digite o tam da seq: "))
conta_par = 0 # Contador de números pares encontrados.
while n > 0:
num = int(input("Digite um num da seq: "))
if num % 2 == 0: # Testa se num é par.
conta_par = conta_par + 1
n = n - 1
print("Quant. pares =", conta_par)
# Fim do programa.
6 -2 7 0 -5 8 4
o seu programa deve escrever o
número 4 para o número de pares e
2 para o de ímpares.
Uma primeira solução é apresentada abaixo, usando a estrutura condicional composta.
n = int(input("Digite o tam da seq: "))
conta_par = 0 # Contador de números pares encontrados.
conta_imp = 0 # Contador de números ímpares encontrados.
while n > 0:
num = int(input("Digite um num da seq: "))
if num % 2 == 0: #par
conta_par = conta_par + 1
else: #ímpar
conta_imp = conta_imp + 1
n = n - 1
print("Quant. pares =", conta_par)
print("Quant. ímpares =", conta_imp)
# Fim do programa.
Note que podemos evitar o comando condicional composto na resolução desse problema, dado que a quantidade de números ímpares pode ser obtida por exclusão, subtraindo-se do total o número de pares encontrados.
n = int(input("Digite o tam da seq: "))
n_salvo = n
conta_par = 0 # Contador de números pares encontrados.
while n > 0:
num = int(input("Digite um num da seq: "))
if num % 2 == 0: #par
conta_par = conta_par + 1
n = n - 1
print("Quant. pares =", conta_par)
print("Quant. ímpares =", n_salvo - conta_par)
# Fim do programa.
Solução:
A estratégia aqui adotada é ler o número n como um inteiro e dividi-lo sucessivamente por 10 até que o resultado seja zero.
Durante o processo de divisões sucessivas, vamos nos desfazendo gradualmente dos dígitos menos significativos em direção aos mais significativos, obtendo cada um dos dígitos pelo uso do operador de resto de divisão por 10 e contabilizando o número de ocorrências do valor em d.
n = int(input("Digite o valor de n: "))
d = int(input("Digite um dígito [0,9]: "))
num = n
cont = 0
while n != 0:
r = n % 10
if r == d:
cont = cont + 1
n = n // 10
print(d,"ocorre",cont,"vezes em",num)
Solução:
#Inverte dígitos:
n = int(input("Digite o valor de n: "))
inv = 0 # variável que irá armazenar o valor de n com os dígitos invertidos.
while n != 0:
r = n % 10
n = n // 10
inv = inv * 10
inv = inv + r
print("Invertido:", inv)
Solução 1:
n = int(input("Digite o valor de n: "))
i = 1
while i*(i+1)*(i+2) < n:
i = i + 1
if i*(i+1)*(i+2) == n:
print("É triangular, ",i,"*",i+1,"*",i+2,"=",n,sep="")
else:
print("Não é triangular")
Solução 2:
Uma segunda versão mais elaborada com códigos de formatação no print.
n = int(input("Digite o valor de n: "))
i = 1
while i*(i+1)*(i+2) < n:
i = i + 1
if i*(i+1)*(i+2) == n:
print("É triangular, %d*%d*%d=%d" %(i,i+1,i+2,n))
else:
print("Não é triangular")
Exemplo: raiz de 9801 = 99 = 98 + 01.
Portanto 9801 é um dos números a ser impresso.
i = 1000
while i <= 9999:
d1 = i%100
d2 = i//100
if (d1+d2)*(d1+d2) == i:
print("Raiz de",i,"é",d1+d2)
i = i + 1
+=,-=,*=,/=,%=.float(), que converte de str para float./ e // e como % se comporta com float.if-elif-else.
| Operador | Exemplo | É equivalente a: |
|---|---|---|
*= | x *= 5 | x = x * 5 |
/= | x /= 5 | x = x / 5 |
%= | x %= 5 | x = x % 5 |
+= | x += 5 | x = x + 5 |
-= | x -= 5 | x = x - 5 |

Dados dois inteiros x e y,
indicar se eles são iguais ou qual é o maior entre eles.
Na solução abaixo, isolamos o caso em que
x é estritamente menor do que y no primeiro if.
Na sequência (no corpo do else), temos dois casos remanescentes, isto é, ou x é o maior dos valores ou eles são iguais. Para distinguir entre esses
dois casos podemos usar um segundo comando condicional dentro do primeiro else.
if x < y :
print("x é menor do que y.")
else:
if x > y :
print("x é maior do que y.")
else:
print("x e y são iguais.")
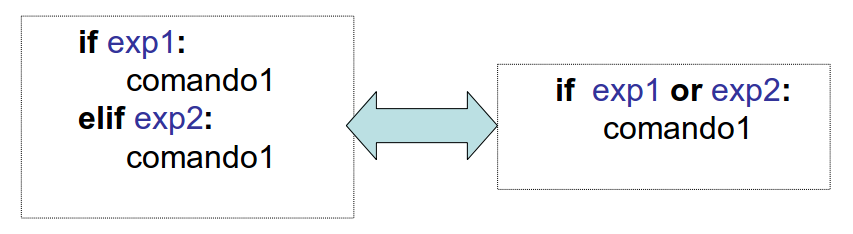
O mesmo efeito pode ser obtido considerando a construção if-elif-else.
if x < y :
print("x é menor do que y.")
elif x > y :
print("x é maior do que y.")
else:
print("x e y são iguais.")
n, n > 0, e uma sequência com n notas finais de MAC2166, determinar quantos alunos:
6 2.3 3 5.0 6.5 8.7 4.9
o resultado deve ser
Número de alunos excelentes = 1Número de alunos aprovados = 3Número de alunos de recuperação = 2Número de alunos reprovados = 1Uma primeira solução é apresentada abaixo.
n = int(input("Digite a quantidade de alunos: "))
no_aprovados = 0
no_recuperacao = 0
no_reprovados = 0
no_excelentes = 0
i = 0
while i < n:
nota = float(input("Digite uma nota: "))
if nota >= 5.0:
no_aprovados += 1
if nota >= 8.0:
no_excelentes += 1
else:
if nota >= 3.0:
no_recuperacao += 1
else:
no_reprovados += 1
i = i + 1
print("Número de alunos excelentes =",no_excelentes)
print("Número de alunos aprovados =",no_aprovados)
print("Número de alunos de recuperação =",no_recuperacao)
print("Número de alunos reprovados =",no_reprovados)
O mesmo efeito pode ser obtido considerando a construção if-elif-else.
n = int(input("Digite a quantidade de alunos: "))
no_aprovados = 0
no_recuperacao = 0
no_reprovados = 0
no_excelentes = 0
i = 0
while i < n:
nota = float(input("Digite uma nota: "))
if nota >= 5.0:
no_aprovados += 1
if nota >= 8.0:
no_excelentes += 1
elif nota >= 3.0:
no_recuperacao += 1
else:
no_reprovados += 1
i = i + 1
print("Número de alunos excelentes =",no_excelentes)
print("Número de alunos aprovados =",no_aprovados)
print("Número de alunos de recuperação =",no_recuperacao)
print("Número de alunos reprovados =",no_reprovados)
bool;True e False;and, or e not;
Python possui 3 operadores chamados lógicos,
que fazem operações com valores booleanos (True e False):

Os operadores lógicos and e or são operadores binários (necessitam de dois operandos, ou seja, dois valores para operar). Eles são usados para combinar condições simples (ex: saída de operadores relacionais) ou o resultado de outros operadores lógicos, de modo a criar operações lógicas mais complexas.
O operador not ('não/negação' em português) é um operador unário. Seu resultado é sempre o inverso (a negação) do operando.
Sejam exp1 e exp2 expressões resultando em valores booleanos (True ou False), temos então:

As tabelas abaixo mostram os resultados dos três operadores lógicos Python para todas possíveis
combinações de seus valores de entrada.
A | B | A and B | A or B |
|---|---|---|---|
False | False | False | False |
False | True | False | True |
True | False | False | True |
True | True | True | True |
A | not A |
|---|---|
False | True |
True | False |


Solução 1: Sem o uso de operadores lógicos
if a > b:
if a > c:
print("a é o maior")
else:
print("c é o maior")
else:
if b > c:
print("b é o maior")
else:
print("c é o maior")
Solução 2: Solução mais compacta com o uso de operadores lógicos
if a > b and a > c :
print("a é o maior")
elif b > c :
print("b é o maior")
else:
print("c é o maior")
| Propriedades Comutativas | A and B = B and A | A or B = B or A |
|---|---|---|
| Propriedades Distributivas | A and (B or C) = (A and B) or (A and C) | A or (B and C) = (A or B) and (A or C) |
| Propriedades Associativas | (A or B) or C = A or (B or C) | (A and B) and C = A and (B and C) |
| Propriedades Idempotentes | A and A = A | A or A = A |
| Dupla Negação | not not A = A | |
| Elementos Absorventes | A or True = True | A and False = False |
| Elementos Neutros | A or False = A | A and True = A |
| Leis de De Morgan | not (A or B) = (not A) and (not B) | not (A and B) = (not A) or (not B) |
Abaixo é apresentado um exemplo de manipulação de uma expressão, usando as propriedades acima listadas, de modo a trocar um operador or por um operador and.
(x < 3) or (y == 0)
Podemos aplicar a dupla negação sem alterar seu resultado:
not not ((x < 3) or (y == 0))
Podemos agora trocar o operador or pelo operador and, aplicando a "Leis de De Morgan":
not (not (x < 3) and not (y == 0))
Finalmente, podemos então simplificar a expressão, trocando os operadores relacionais negados por operadores relacionais complementares:
not (x >= 3 and y != 0)
and se escreve como &&
e o operador lógico or como ||.
Em linguagem C, os valores booleanos False e True
são definidos como os valores numéricos 0 e 1, respectivamente.
Isso significa que o mesmo efeito do operador lógico and pode
ser obtido em C através de um simples produto, isto é, A && B
pode ser obtido como A * B. Porém, observe que a multiplicação
possui maior nível de precedência, o que pode gerar alterações na ordem de
execução no caso de expressões mais complexas, consequentemente levando a um resultado
diferente do esperado.
Já no caso do operador lógico or temos que
A || B pode ter o seu efeito reproduzido pela expressão A+B-A*B.
No Python 3, o tipo bool de dados booleanos é uma subclasse dos inteiros.
Logo, no Python 3, os valores booleanos False e True se comportam como os valores 0 e 1, respectivamente, em quase todos os contextos, a exceção é que, quando convertidos em uma string, as strings "False" ou "True" são retornadas, respectivamente.
Experimente digitar no prompt (>>>) do Python shell os comandos abaixo:
>>> 1 == TrueTrue>>> 0 == TrueFalse>>> 0 == FalseTrue>>> 1 == FalseFalse>>> str(1)'1'>>> str(True)'True'>>> str(0)'0'>>> str(False)'False'
Solução 1: Sem o uso de operadores lógicos
# Primeira data.
d1 = int(input("Dia: "))
m1 = int(input("Mês: "))
a1 = int(input("Ano: "))
# Segunda data.
d2 = int(input("Dia: "))
m2 = int(input("Mês: "))
a2 = int(input("Ano: "))
if a1 > a2:
print("Data1 é maior!")
elif a1 == a2:
if m1 > m2:
print("Data1 é maior!")
elif m1 == m2:
if d1 > d2:
print("Data1 é maior!")
elif d1 == d2:
print("Datas são iguais!")
else:
print("Data2 é maior!")
else:
print("Data2 é maior!")
else:
print("Data2 é maior!")
Solução 2: Solução mais compacta com o uso de operadores lógicos
# Primeira data.
d1 = int(input("Dia: "))
m1 = int(input("Mês: "))
a1 = int(input("Ano: "))
# Segunda data.
d2 = int(input("Dia: "))
m2 = int(input("Mês: "))
a2 = int(input("Ano: "))
if a1>a2 or (a1==a2 and m1>m2) or (a1==a2 and m1==m2 and d1>d2):
print("Data1 é maior!")
elif a1==a2 and m1==m2 and d1==d2:
print("Datas são iguais!")
else:
print("Data2 é maior!")
Solução 3:
Segundo a propriedade distributiva
da álgebra booleana temos:
expr1 and (expr2 or expr3) = (expr1 and expr2) or (expr1 and expr3)Logo, uma outra solução pode ser obtida colocando a condição a1==a2 em evidência:
# Primeira data.
d1 = int(input("Dia: "))
m1 = int(input("Mês: "))
a1 = int(input("Ano: "))
# Segunda data.
d2 = int(input("Dia: "))
m2 = int(input("Mês: "))
a2 = int(input("Ano: "))
if a1>a2 or (a1==a2 and (m1>m2 or (m1==m2 and d1>d2))):
print("Data1 é maior!")
elif a1==a2 and m1==m2 and d1==d2:
print("Datas são iguais!")
else:
print("Data2 é maior!")
Solução 1:
Uma solução usando operadores lógicos:
n = int(input("Digite n: "))
rec = 0
i = 1
while i <= n:
nota = float(input("Digite uma nota: "))
if 3.0 <= nota and nota < 5.0:
rec = rec + 1
i = i + 1
print(rec,"alunos ficaram de recuperação")
Do ponto de vista gráfico, usando a notação de conjuntos de intervalos na reta dos reais, temos:


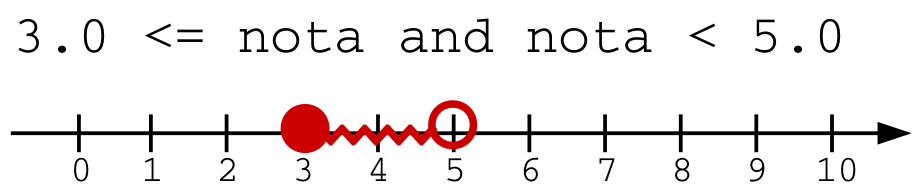
Observe que graficamente o operador lógico "and"
possui o efeito de intersecção dos conjuntos.
Solução 2:
Uma segunda solução sem usar operadores lógicos:
n = int(input("Digite n: "))
rec = 0
i = 1
while i <= n:
nota = float(input("Digite uma nota: "))
if nota >= 3.0:
if nota < 5.0:
rec = rec + 1
i = i + 1
print(rec,"alunos ficaram de recuperação")
Solução 3:
O Python ainda permite uma terceira solução, na qual o intervalo numérico é especificado de modo mais similar a nossa linguagem, usando operadores de comparação de forma encadeada:
n = int(input("Digite n: "))
rec = 0
i = 1
while i <= n:
nota = float(input("Digite uma nota: "))
if 3.0 <= nota < 5.0:
rec = rec + 1
i = i + 1
print(rec,"alunos ficaram de recuperação")
No entanto, essa versão não é recomendada por não possuir
um padrão equivalente em outras linguagens,
o que pode gerar erros ao transcrever a solução para outras linguagens. Um exemplo desse erro no caso da linguagem C é explicado no quadro de curiosidades abaixo.
30 <= nota < 50 para testar se a nota está no intervalo de recuperação não produz o efeito desejado. No entanto, ela não gera um erro de sintaxe e sim um erro de lógica, sendo, portanto, mais difícil de localizar e corrigir.
#include <stdio.h>
int main(){
float nota;
int rec;
nota = 8.0;
rec = 3.0 <= nota < 5.0;
if(rec)
printf("Ficou de recuperação!\n");
return 0;
}
Vamos analisar o comando rec = 3.0 <= nota < 5.0;
da sétima linha do código acima. Com exceção do ponto e vírgula presente no final do comando,
que faz parte da sintaxe da linguagem C, o resto da linha é praticamente idêntico a um código em Python.
Em linguagem C, os operadores relacionais são operadores binários, que operam sobre dois operandos e que produzem como saída 0 ou 1, representando False ou True, respectivamente.
Como na sétima linha do código temos
dois operadores relacionais (<= e <) que possuem o mesmo nível de precedência, eles são executados
da esquerda para a direita.
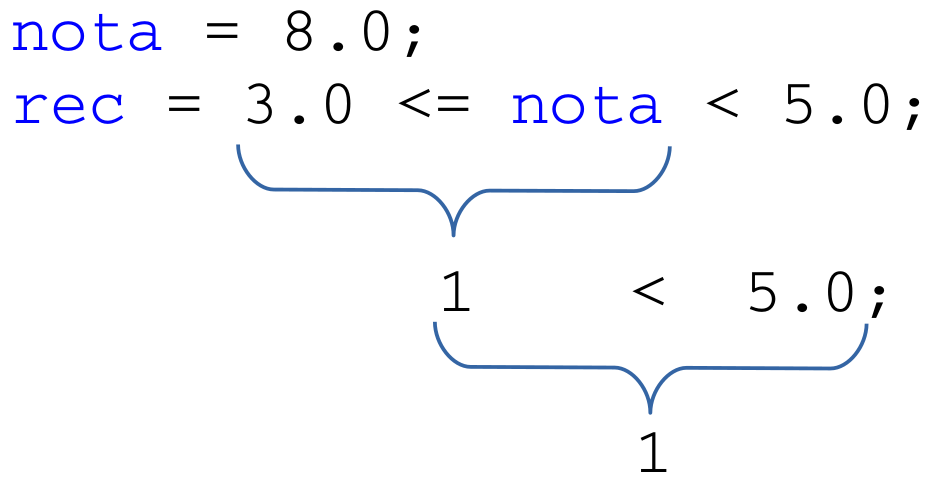
Portanto, primeiramente executamos o operador "Menor ou igual a" (<=), comparando 3.0 com o valor 8.0 em nota, o que produzirá 1 (verdadeiro). Esse valor resultante 1
será então comparado pelo operador < com o 5.0,
produzindo 1 (verdadeiro) como saída. Ou seja, o aluno com nota 8.0
será considerado indevidamente como estando de recuperação, segundo o código acima. Portanto, para testar intervalos em C,
precisamos necessariamente do uso do operador lógico "and" (que em C é escrito como &&).
Para o exemplo acima, a construção correta em C seria:
rec = 3.0 <= nota && nota < 5.0;
0 2 3 4 6 8
# dados de entrada
print("Cálculo dos n primeiros múltiplos de i ou de j")
n = int(input("Digite n: "))
i = int(input("Digite i: "))
j = int(input("Digite j: "))
cont = 0 #conta quantos múltiplos foram impressos.
cm = 0 #candidato a múltiplo.
while cont < n:
if cm%i == 0 or cm%j == 0:
print(cm)
cont += 1
cm += 1
Segunda solução:
Mais elaborada. Faz menos iterações que a anterior.
A cada iteração imprime um múltiplo de i ou j.
# dados de entrada
print("Cálculo dos n primeiros múltiplos de i ou de j")
n = int(input("Digite n: "))
i = int(input("Digite i: "))
j = int(input("Digite j: "))
multi = 0 # múltiplos de i
multj = 0 # múltiplos de j
cont = 0 # conta quantos múltiplo foram impressos
while cont < n:
if multi < multj:
print(multi)
multi += i
elif multj < multi:
print(multj)
multj += j
else: # multi == multj
print(multj)
multi += i
multj += j
cont += 1
n = int(input("Digite o tam da seq: "))
ant = int(input("Digite um num da seq: "))
cresce = True
i = 2
while i <= n and cresce:
num = int(input("Digite um num da seq: "))
if num <= ant:
cresce = False
ant = num
i = i + 1
if cresce:
print("Sequência crescente")
else:
print("Sequência não é crescente")
n = int(input("Digite o valor de n: "))
adjiguais = False
ant = n%10
n = n//10
while n > 0:
r = n%10
if ant == r:
adjiguais = True
ant = r
n = n//10
if adjiguais:
print("Contém adjacentes iguais")
else:
print("Não contém adjacentes iguais")
Uma segunda solução usando uma condição extra de parada do laço.
n = int(input("Digite o valor de n: "))
adjiguais = False
ant = n%10
n = n//10
while n > 0 and not adjiguais:
r = n%10
if ant == r:
adjiguais = True
ant = r
n = n//10
if adjiguais:
print("Contém adjacentes iguais")
else:
print("Não contém adjacentes iguais")
Outra solução alternativa, inicializando a variável ant
com um dígito inválido, ao invés de ler o primeiro
dígito de n fora do laço.
Com essa alteração, a condição do laço ant == r
nunca será verdadeira na primeira iteração do laço.
n = int(input("Digite o valor de n: "))
adjiguais = False
ant = 10
while n > 0 and not adjiguais:
r = n%10
if ant == r:
adjiguais = True
ant = r
n = n//10
if adjiguais:
print("Contém adjacentes iguais")
else:
print("Não contém adjacentes iguais")
n = int(input("Digite n: "))
a1 = int(input("Digite um num: "))
i = 1
if n > 1:
a2 = int(input("Digite um num: "))
i = 2
r = a2 - a1 #razão da PA
ant = a2
pa = True
while i < n:
ai = int(input("Digite um num: "))
if ai - ant != r:
pa = False
ant = ai
i += 1
if pa and n > 1:
print("A sequência é uma P.A. de razão",r)
elif pa:
print("A sequência é uma P.A.")
else:
print("A sequência não é uma P.A.")
Um número natural é um número primo quando ele tem exatamente dois divisores naturais distintos: o número um e ele mesmo. Por definição, 0 e 1 não são números primos.
Primeira solução: Um número primo n não pode ser divisível por nenhum outro número no intervalo [2,n-1]. Logo, testamos todos candidatos a divisores possíveis no intervalo [2,n-1], e usamos um indicador de passagem (variável primo) para sinalizar a ocorrência desse evento (divisão). Ao final do programa vale que primo == False se e somente se o número dado não é primo.
print("Teste de primalidade")
n = int(input("Digite um inteiro: "))
# o número é primo até que se prove o contrário
primo = True #indicador de passagem
d = 2 #os candidatos a divisores positivos de n
while d < n:
if n%d == 0:
primo = False # não é primo!
d += 1
if n <= 1: #nenhum número natural <= 1 é primo.
primo = False
if primo:
print("O número é primo")
else:
print("O número não é primo")
Segunda solução: Reduz o espaço de busca, testando apenas os candidatos a divisores positivos de n no intervalo 2,3,4,...,n/2.
print("Teste de primalidade")
n = int(input("Digite um inteiro: "))
if n <= 1: #nenhum número natural <= 1 é primo.
primo = False
else:
# o número é primo até que se prove o contrário.
primo = True #indicador de passagem
d = 2 #os candidatos a divisores positivos de n.
while d <= n//2 and primo:
if n%d == 0:
primo = False # não é primo!
d += 1
if primo:
print("O número é primo")
else:
print("O número não é primo")
Terceira solução: Reduz o espaço de busca ainda mais. Testa se o número é par fora do laço principal. Dentro do while só testa candidatos a divisores ímpares.
print("Teste de primalidade")
n = int(input("Digite um inteiro: "))
if n <= 1: #nenhum número natural <= 1 é primo.
primo = False
elif n%2 == 0 and n > 2:
primo = False #nenhum número par > 2 é primo.
else:
# o número é primo até que se prove o contrário
# vale que n é um ímpar maior que 1 ou é 2.
primo = True #indicador de passagem
d = 3 #os candidatos a divisores positivos de n são 3,5,7,...,n/2
while d <= n//2 and primo:
if n%d == 0:
primo = False # não é primo!
d += 2
if primo:
print("O número é primo")
else:
print("O número não é primo")
Outras possíveis otimizações podem ser encontradas aqui.
9 8 7 6 5 4 3 2 1 8 7 6 5 4 3 2 1 7 6 5 4 3 2 1 6 5 4 3 2 1 5 4 3 2 1 4 3 2 1 3 2 1 2 1 1
n = int(input("Digite n: "))
j = n
while j > 0:
i = j
while i > 0:
print(i,end=" ")
i -= 1
print()
j -= 1

soma = 0
i = 1
while i <= n:
j = 1
while j <= m:
#numerador:
num = i*i*j
#denominador:
den = (3**i)*(j*(3**i) + i*(3**j))
soma += num/den
j += 1
i += 1
print("Soma:",soma)
Uma solução alternativa pode ser obtida
através da manipulação
dos somatórios:
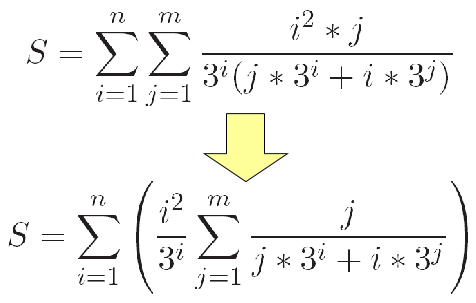
soma = 0
i = 1
while i <= n:
somaj = 0
pi = 3**i
j = 1
while j <= m:
somaj += j/(j*pi + i*(3**j))
j += 1
soma += (i*i/pi)*somaj
i += 1
print("Soma:",soma)
Solução:
n = int(input("Digite n: "))
print("Decomposição de",n,"em fatores primos:")
fator = 2
while n > 1:
mult = 0
while n % fator == 0:
n = n // fator
mult += 1
if mult > 0:
print("fator",fator,"multiplicidade",mult)
fator += 1
Uma explicação dessa solução pode ser encontrada no vídeo abaixo:
Dado um número inteiro m, m>0, determinar os ímpares consecutivos cuja soma é igual a n3, para n assumindo valores de 1 a m.
Solução 1:
m = int(input("Digite m: "))
n = 1
while n <= m:
inic = 1
soma = 0
while soma != n*n*n:
soma = 0
i = 1
while i <= n:
soma += inic + (i-1)*2
i += 1
inic += 2
inic -= 2
print(n*n*n,"=",end=" ")
print(inic, end=" ")
i = 2
while i <= n:
print("+",inic + (i-1)*2, end=" ")
i += 1
print()
n += 1
Solução 2:
Evita o laço mais interno, aplicando a fórmula
da soma dos termos da PA.
m = int(input("Digite m: "))
n = 1
while n <= m:
inic = 1
soma = 0
while soma != n*n*n:
soma = ((inic + inic+(n-1)*2)*n)//2
inic += 2
inic -= 2
print(n*n*n,"=",end=" ")
print(inic, end=" ")
i = 2
while i <= n:
print("+",inic + (i-1)*2, end=" ")
i += 1
print()
n += 1
Solução 3:
Solução praticamente idêntica a anterior.
Apenas foram mudadas a ordem de alguns comandos e a
inicialização de inic, de modo a evitar
o comando inic -= 2 após o laço mais interno.
m = int(input("Digite m: "))
n = 1
while n <= m:
inic = -1
soma = 0
while soma != n*n*n:
inic += 2
soma = ((inic + inic+(n-1)*2)*n)//2
print(n*n*n,"=",end=" ")
print(inic, end=" ")
i = 2
while i <= n:
print("+",inic + (i-1)*2, end=" ")
i += 1
print()
n += 1
Solução 4:
Solução mais compacta,
aproveitando o fato de que o último termo
de uma sequência e o início da próxima
são ímpares consecutivos.
Por exemplo, observe que a sequência do 2 elevado ao cubo termina em 5,
enquanto que a sequência do 3 elevado ao cubo começa no 7 = 5+2.
m = int(input("Digite m: "))
n = 1
imp = 1 #primeiro dos ímpares de uma sequência que soma n^3
while n <= m:
print(n*n*n,"=",end=" ")
print(imp, end=" ")
i = 2
while i <= n:
imp += 2
print("+",imp, end=" ")
i += 1
print()
imp += 2 #início da próxima sequência
n += 1
Vamos agora provar a validade da solução acima. Isto é, vamos demonstrar que, de fato, o último termo de uma sequência e o início da próxima são ímpares consecutivos.
![]()
Os n ímpares consecutivos formam uma progressão
aritmética (PA) de razão 2 (R=2).
Logo, podemos usar a fórmula do termo geral da PA:
ai = a1 + (i-1)*R.
![]()
Além disso, podemos aplicar a fórmula da soma dos termos da PA:
![]()
Combinando a fórmula da soma dos termos da PA com a fórmula do termo geral para o n-ésimo termo, temos:
![]()
Dado que sabemos que a1 é um número ímpar, podemos escrevê-lo na forma a1 = k*2+1, em que k é um número inteiro.
![]()
Portanto, temos que:
![]()
Isolando k, temos que:
![]()
Portanto, a1 pode ser calculado por:
![]() (*)
(*)
Aplicando a fórmula do termo geral para o n-ésimo termo, temos então:
![]()
O início da próxima sequência pode então ser calculado, trocando-se n por n+1 na equação (*):
![]()
Ou seja, temos acima um valor igual a an + 2, como se queria demonstrar.
Solução 5:
Uma quinta solução pode ser obtida
calculando-se o início de cada sequência
diretamente através da equação (*) (isto é, a1 = n2 - n + 1) para cada valor de n.
A escrita do código Python desta quinta solução fica como exercício para o leitor.
Na figura, no plano cartesiano, a região sombreada não inclui as linhas de bordo. Note que o eixo y cai bem no meio da figura, e usamos o lado do quadrado para indicar as ordenadas correspondentes.
Escreva um programa que lê as coordenadas cartesianas (x, y) de um ponto, ambas do tipo float e imprime dentro se esse ponto está na região, e fora caso contrário.
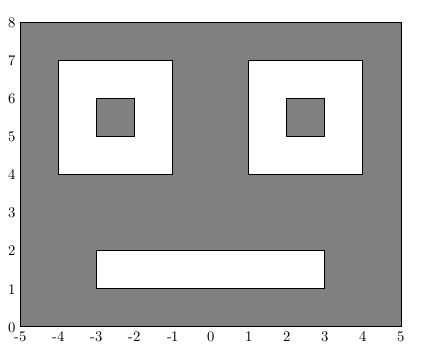
Solução 1:
x = float(input("Digite x: "))
y = float(input("Digite y: "))
# suponha que (x,y) está dentro
dentro = True
if x <= -5 or 5 <= x or y <= 0 or 8 <= y:
# aqui sabemos que (x,y) está fora da face
dentro = False
elif -3 <= x <= 3 and 1 <= y <= 2:
# aqui sabemos que (x,y) está na boca
dentro = False
elif -4 <= x <= -1 and 4 <= y <= 7:
# aqui sabemos que (x,y) está no olho esquerdo
dentro = False
if -3 < x < -2 and 5 < y < 6:
# aqui sabemos que na verdade (x,y) está na iris esquerda
dentro = True
elif 1 <= x <= 4 and 4 <= y <= 7:
# aqui sabemos que (x,y) está no olho direito
dentro = False
if 2 < x < 3 and 5 < y < 6:
# aqui sabemos que na verdade (x,y) está na iris direita
dentro = True
if dentro:
print("dentro")
else:
print("fora")
Solução 2:
#começa supondo que está fora e depois... A variável dentro e um indicador de passagem bool.
x = float(input("Digite x: "))
y = float(input("Digite y: "))
# suponha que (x,y) está fora
dentro = False
if -5 < x < 5 and 0 < y < 8:
# aqui sabemos que (x,y) está na face
dentro = True
if -3 <= x <= 3 and 1 <= y <= 2:
# aqui sabemos que (x,y) está na face, mas está na boca
dentro = False
elif -4 <= x <= -1 and 4 <= y <= 7:
# aqui sabemos que (x,y) está no olho esquerdo
dentro = False
if -3 < x < -2 and 5 < y < 6:
# aqui sabemos que na verdade (x,y) está na iris esquerda
dentro = True
elif 1 <= x <= 4 and 4 <= y <= 7:
# aqui sabemos que (x,y) está no olho direito
dentro = False
if 2 < x < 3 and 5 < y < 6:
# aqui sabemos que na verdade (x,y) está na iris direita
dentro = True
if dentro:
print("dentro")
else:
print("fora")
Solução 3:
x_pos = x = float(input("Digite x: "))
y = float(input("Digite y: "))
if x < 0: # simetria ;-)
x_pos = -x
# suponha que (x,y) que está dentro
dentro = True
if x_pos >= 5 or y >= 8 or y <= 0:
# aqui sabemos que (x,y) está fora da face
dentro = False
elif x_pos <= 3 and 1 <= y <= 2:
# aqui sabemos que (x,y) está na boca
dentro = False
elif 1 <= x_pos <= 4 and 4 <= y <= 7:
# aqui sabemos que (x,y) está em um olho
if not (2 < x_pos < 3 and 5 < y < 6):
# aqui sabemos que (x,y) está fora da iris
dentro = False
if dentro:
print("dentro")
else:
print("fora")
Solução 4:
x_pos = x = float(input("Digite x: "))
y = float(input("Digite y: "))
if x < 0:
x_pos = -x
# face == True se (x,y) está na face
face = x_pos < 5 and 0 < y < 8
# boca == True se (x,y) está na boca
boca = x_pos <= 3 and 1 <= y <= 2
# olho == True se (x,y) está em um dos olhos
olho = 1 <= x_pos <= 4 and 4 <= y <= 7
# iris == True se (x,y) está em uma das iris
iris = 2 < x_pos < 3 and 5 < y < 6
# vixe! :-D complicado?! certamente muito elegante
if iris or face and not (boca or olho):
print("dentro")
else:
print("fora")
Uma função é uma unidade de código de programa autônoma desenhada para cumprir uma tarefa particular.
A chamada de uma função desvia a execução do código para o corpo da função (bloco de código da função):
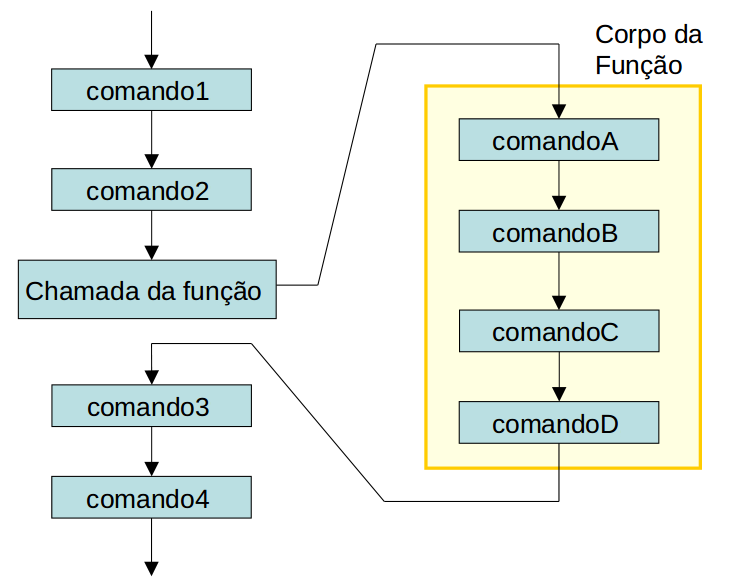
fatorial(n) que
recebe um inteiro n e devolve o fatorial de n.n e k e calcula o
coeficiente binomial, do número n,
na classe k, isto é,
o número de combinações de n
termos, k a k, dado por n!/(k!(n-k)!).
Escreva essa função usando a função
fatorial(n) do item anterior.n, com n > 0, e que imprime o Triângulo de Pascal com n linhas.
Exemplo: para n = 5, o programa deve escrever:
1 1 11 2 1 1 3 3 1 1 4 6 4 1
def fatorial(n):
fat = 1
i = 2
while i <= n:
fat *= i
i += 1
return fat
def binomial(n,k):
return fatorial(n)//(fatorial(k)*fatorial(n-k))
def main():
print("Triângulo de Pascal")
n = int(input("Digite o número de linhas: "))
i = 0
while i < n:
j = 0
while j <= i:
b = binomial(i,j)
print("%3d "%b,end="")
j+= 1
print()
i += 1
main()
Faça um programa que lê um número inteiro n,
com n > 0, e para cada número entre 1 e n indica
se ele é soma de dois primos.
Por exemplo, para n = 8 o programa deve escrever
1 não é soma de primos2 não é soma de primos3 não é soma de primos4 é soma dos primos 2 e 25 é soma dos primos 2 e 36 é soma dos primos 3 e 37 é soma dos primos 2 e 58 é soma dos primos 3 e 5
def primo(n):
div = 2
ehprimo = True
while div < n:
if n % div == 0:
ehprimo = False
div += 1
if n <= 1:
ehprimo = False
return ehprimo
def main():
n = int(input("Digite n: "))
i = 1
while i <= n:
encontrou = False
j = 2
while j < i and not encontrou:
if primo(j) and primo(i-j):
encontrou = True
p1 = j
p2 = i-j
j += 1
if encontrou:
print("%d é soma dos primos %d e %d"%(i,p1,p2))
else:
print("%d não é soma de primos"%i)
i += 1
main()
Em Python, existem várias funções matemáticas prontas do
módulo math. Um exemplo de função desse módulo é a
factorial, que calcula o fatorial de um número.
Para usar uma função do módulo math, devemos primeiramente
importar o módulo no código, usando o comando import math, e
depois chamar a função. O exemplo abaixo mostra uma chamada à
função factorial.
import math
n = int(input("Digite o valor de n: "))
fat = math.factorial(n)
print("Fatorial de",n,"é",fat)
math.sqrt(x) do
módulo de matemática da linguagem Python
(import math), escreva uma função que
recebe as coordenadas cartesianas de dois pontos no plano e
devolve a distância entre os pontos.(x0, y0) e uma sequência de n > 1
pontos e determina o ponto mais próximo do ponto origem.
import math
def distancia(x1,y1,x2,y2):
return math.sqrt((x2-x1)**2 + (y2-y1)**2)
def main():
print("Digite as coordenadas do ponto de origem", end="")
x0 = float(input("x: "))
y0 = float(input("y: "))
n = int(input("Digite a quantidade de pontos: "))
print("Digite as coordenadas de um novo ponto", end="")
x_menor = float(input("x: "))
y_menor = float(input("y: "))
menor_distancia = distancia(x_menor,y_menor,x0,y0)
while n>1:
print("Digite as coordenadas de um novo ponto", end="")
x = float(input("x: "))
y = float(input("y: "))
d = distancia(x,y,x0,y0)
if d < menor_distancia:
x_menor = x
y_menor = y
menor_distancia = d
n -= 1
print("O ponto mais próximo de (%.2f,%.2f) é (%.2f,%.2f)" %(x0,y0,x_menor,y_menor))
main()
O MDC de dois números inteiros é o maior número inteiro que divide ambos sem deixar resto.
Exemplos:Algoritmo de Euclides: Para dois números A e B:
def MDC(a, b):
if a < b:
a,b = b,a
while b > 0:
r = a % b
a = b
b = r
return a
def main():
print("MDC entre a e b:")
a = int(input("Digite a: "))
b = int(input("Digite b: "))
print("MDC =", MDC(a,b))
main()
Dados um número inteiro n>0 e uma sequência com n números inteiros maiores do que zero, determinar o máximo divisor comum entre eles. Por exemplo, para a entrada
3 42 30 105o seu programa deve escrever o número 3.
DICA: O MDC é uma operação associativa.
Exemplo: MDC(A,B,C,D) = MDC(MDC(A,B),C,D) = MDC(MDC(MDC(A,B),C),D)
def MDC(a, b):
if a < b:
a,b = b,a
while b > 0:
r = a % b
a = b
b = r
return a
def main():
n = int(input("Digite n: "))
mdc = int(input("Digite o primeiro número: "))
i = 1
while i < n:
num = int(input("Digite o próximo número: "))
a = mdc
b = num
mdc = MDC(a, b)
i += 1
print("MDC =",mdc)
main()
list, índices, referências, clones,len() e método append();for i in range(início,fim,passo):;for item in lista:.
Até aqui, trabalhamos com variáveis simples, capazes de armazenar apenas um tipo, como bool, float e int.
Uma lista (tipo list) em Python é uma sequência de valores de qualquer tipo ou classe tais como int, float, bool, str e mesmo list, entre outros.
Existem várias maneiras de criarmos uma lista. A maneira mais simples é envolver os elementos da lista por colchetes ([ e ]). Por exemplo, podemos criar uma lista contendo os anos de obtenção das 5 primeiras conquistas do Brasil em Copas do Mundo de Futebol da seguinte maneira:
>>> anos_conquistas = [1958, 1962, 1970, 1994, 2002]
Observe o uso de colchetes de abertura ([) para marcar o início e o
colchetes de fechamento (]) para marcar o final da lista, e os elementos separados
por vígula.
Ao contrário do conceito de vetores em linguagem C, que são coleções indexadas homogêneas de dados (todos elementos do vetor são de um mesmo tipo), as listas em Python podem conter vários tipos de dados, sendo, portanto, possível armazenar coleções heterogêneas de dados.
>>> L = [1958, 1962, 1970, 1994, 2002]
Lista são estruturas sequenciais indexadas pois seus elementos podem ser acessados sequencialmente utilizando índices. Por convenção do Python, o primeiro elemento da lista tem índice 0, o segundo tem índice 1, e assim por diante. Observe que, por começar pelo índice zero, o último elemento da lista anos_conquistas, o ano 2002, tem índice 4, sendo que essa lista tem comprimento 5.
Índices negativos indicarão elementos da direita para a esquerda ao invés de da esquerda para a direita.
Um erro comum em programas é a utilização de índices inválidos.
len().
>>> len(anos_conquistas)5i recebe o valor zero que corresponde ao primeiro índice e, enquanto o índice for menor que o comprimento da lista (= len(primos)), o elemento de índice i é impresso.
n > 0 e uma sequência com n
números reais, imprimí-los na ordem inversa a da leitura.
Dica: Criar uma lista vazia (seq = []) e usar append.
Solução 1:
Vamos fazer do modo tradicional, imprimindo dentro de um while.
n = int(input("Digite n: "))
seq = []
i = 0
while i < n:
num = float(input("Digite o %do. num: "%(i+1)))
seq.append(num)
i += 1
i = n-1
while i >= 0:
print(seq[i])
i -= 1
Solução 2:
Solução alternativa usando índices negativos.
n = int(input("Digite n: "))
seq = []
i = 0
while i < n:
num = float(input("Digite o %do. num: "%(i+1)))
seq.append(num)
i += 1
i = -1
while i >= -n:
print(seq[i])
i -= 1
Solução 3:
Solução alternativa usando o comando for.
n = int(input("Digite n: "))
seq = []
for i in range(n):
num = float(input("Digite o %do. num: "%(i+1)))
seq.append(num)
for i in range(n-1, -1, -1):
print(seq[i])
Solução 4:
Outra solução alternativa usando o comando for
com índices negativos.
n = int(input("Digite n: "))
seq = []
for i in range(n):
num = float(input("Digite o %do. num: "%(i+1)))
seq.append(num)
for i in range(-1, -n-1, -1):
print(seq[i])
Solução 5:
No Python, é possível fazer: print(seq.reverse()).
n = int(input("Digite n: "))
seq = []
for i in range(n):
num = float(input("Digite o %do. num: "%(i+1)))
seq.append(num)
seq.reverse()
for x in seq:
print(x)
n > 0 lançamentos de uma roleta
(números entre 0 e 36), calcular a frequência de cada número.
Dica: Criar uma lista com 37 zeros.
Solução 1:
Solução usando o comando while.
n = int(input("Digite n: "))
freq = []
i = 0
while i < 37:
freq.append(0)
i += 1
i = 0
while i < n:
num = int(input("roleta: "))
freq[num] += 1
i += 1
i = 0
while i < 37:
print("freq.rel.(%d): %f"%(i,freq[i]/n))
i += 1
Solução 2:
Solução mais compacta usando freq = [0]*37
para a criação da lista com 37 zeros.
n = int(input("Digite n: "))
freq = [0]*37
i = 0
while i < n:
num = int(input("roleta: "))
freq[num] += 1
i += 1
i = 0
while i < 37:
print("freq.rel.(%d): %f"%(i,freq[i]/n))
i += 1
Solução 3:
Solução alternativa usando o comando for.
n = int(input("Digite n: "))
freq = [0]*37
for i in range(n):
num = int(input("roleta: "))
freq[num] += 1
i = 0
for x in freq:
print("freq.rel.(%d): %f"%(i,x/n))
i += 1
Solução 4:
Solução alternativa que simula a roleta usando
o gerador de números pseudo-aleatórios do
módulo random do Python,
ao invés de solicitar a entrada manual dos n lançamentos.
import random
n = int(input("Digite n: "))
freq = [0]*37
for i in range(n):
num = random.randrange(0, 37)
freq[num] += 1
i = 0
for x in freq:
print("freq.rel.(%d): %f"%(i,x/n))
i += 1
n > 0 números reais,
imprimi-los eliminando as repetições.
Solução 1:
Solução usando while.
n = int(input("Digite n: "))
seq = []
for i in range(n):
num = float(input("Digite o %do. num: "%(i+1)))
rep = False
j = 0
while j < len(seq) and rep == False:
if seq[j] == num:
rep = True
j += 1
if rep == False: # if not rep:
seq.append(num)
print(seq)
Solução 2:
Solução usando for.
n = int(input("Digite n: "))
seq = []
for i in range(n):
num = float(input("Digite o %do. num: "%(i+1)))
rep = False
for x in seq:
if x == num:
rep = True
if rep == False: # if not rep:
seq.append(num)
print(seq)
Solução 3:
Solução compacta, aproveitando o fato de
que o Python permite testar diretamente se um elemento não faz parte de uma
lista,
através do comando if num not in seq:
n = int(input("Digite n: "))
seq = []
for i in range(n):
num = float(input("Digite o %do. num: "%(i+1)))
if num not in seq:
seq.append(num)
print(seq)
n
e m e duas sequências ordenadas com n > 0
e m > 0 números inteiros, criar uma lista
contendo a sequência ordenada com todos os elementos das
duas sequências originais sem repetição.Sugestão: Imagine uma situação real, por exemplo, dois fichários de uma biblioteca.
Solução 1:
Cada sequência ordenada fornecida é lida em uma
lista correspondente já eliminando possíveis elementos repetidos,
usando a solução empregada no problema anterior.
As duas listas resultantes seq1 e seq2 são então percorridas, usando as variáveis i e j como seus respectivos índices, copiando de modo intercalado para uma lista de saída seq3 sempre o menor valor entre seq1[i] e seq2[j].
n = int(input("Digite n: "))
seq1 = []
for i in range(n):
num = int(input("Digite o %do. num: "%(i+1)))
if num not in seq1:
seq1.append(num)
m = int(input("Digite m: "))
seq2 = []
for i in range(m):
num = int(input("Digite o %do. num: "%(i+1)))
if num not in seq2:
seq2.append(num)
seq3 = []
i,j = 0,0
while i < len(seq1) and j < len(seq2):
if seq1[i] < seq2[j]:
seq3.append(seq1[i])
i += 1
elif seq2[j] < seq1[i]:
seq3.append(seq2[j])
j += 1
else: # seq1[i] == seq2[j]
seq3.append(seq1[i])
i += 1
j += 1
while i < len(seq1):
seq3.append(seq1[i])
i += 1
while j < len(seq2):
seq3.append(seq2[j])
j += 1
print(seq3)
Solução 2:
Solução similar à anterior,
porém durante o processo de intercalação,
os casos em que i ou j excedem
o último índice válido de suas respectivas listas
é tratado diretamente dentro do mesmo laço que
trata os demais casos em que os dois índices são válidos.
n = int(input("Digite n: "))
seq1 = []
for i in range(n):
num = int(input("Digite o %do. num: "%(i+1)))
if num not in seq1:
seq1.append(num)
m = int(input("Digite m: "))
seq2 = []
for i in range(m):
num = int(input("Digite o %do. num: "%(i+1)))
if num not in seq2:
seq2.append(num)
seq3 = []
i,j = 0,0
while i < len(seq1) or j < len(seq2):
if i == len(seq1):
seq3.append(seq2[j])
j += 1
elif j == len(seq2):
seq3.append(seq1[i])
i += 1
elif seq1[i] < seq2[j]:
seq3.append(seq1[i])
i += 1
elif seq2[j] < seq1[i]:
seq3.append(seq2[j])
j += 1
else: # seq1[i] == seq2[j]
seq3.append(seq1[i])
i += 1
j += 1
print(seq3)
Solução 3:
Idêntica à solução anterior, exceto que exploramos o fato de que as duas sequências fornecidas estão ordenadas, de modo que para eliminar seus elementos repetidos durante o laço de leitura, basta comparar com o último valor já lido na lista.
n = int(input("Digite n: "))
num = int(input("Digite o 1o. num: "))
seq1 = [num]
for i in range(1,n):
num = int(input("Digite o %do. num: "%(i+1)))
if num != seq1[len(seq1)-1]: #compara com o último valor inserido em seq1.
seq1.append(num)
m = int(input("Digite m: "))
num = int(input("Digite o 1o. num: "))
seq2 = [num]
for i in range(1,m):
num = int(input("Digite o %do. num: "%(i+1)))
if num != seq2[len(seq2)-1]: #compara com o último valor inserido em seq2.
seq2.append(num)
seq3 = []
i,j = 0,0
while i < len(seq1) or j < len(seq2):
if i == len(seq1):
seq3.append(seq2[j])
j += 1
elif j == len(seq2):
seq3.append(seq1[i])
i += 1
elif seq1[i] < seq2[j]:
seq3.append(seq1[i])
i += 1
elif seq2[j] < seq1[i]:
seq3.append(seq2[j])
j += 1
else: # seq1[i] == seq2[j]
seq3.append(seq1[i])
i += 1
j += 1
print(seq3)
+;*;A
a uma segunda variável B não cria uma nova lista.
As duas variáveis estarão referenciando a mesma lista
na memória. Isto significa que alterações na
lista A afetam B e vice-versa:
>>> A = ["Bento Gonçalves", "Campos do Jordão", "Gramado"]>>> B = A>>> B.append("Ouro Preto")>>> print(B)['Bento Gonçalves', 'Campos do Jordão', 'Gramado', 'Ouro Preto']>>> print(A)['Bento Gonçalves', 'Campos do Jordão', 'Gramado', 'Ouro Preto']>>> id(A)139789181142280>>> id(B)139789181142280>>> id(A) == id(B)True>>> A is BTrue
Cada objeto em Python, incluindo listas, possui um identificador exclusivo (número inteiro único) que pode ser acessado usando a função
id() do Python.
Observe que no exemplo acima, as listas A e B possuem o mesmo identificador,
confirmando que elas correspondem à mesma lista na memória.
O teste id(A) == id(B)
pode ser igualmente obtido através do comando
A is B.
Em algumas situações, no entanto,
precisamos, de fato, criar uma réplica/clone na
memória de uma lista existente.
Para isso podemos usar o comando B = list(A).
Note que nesse caso alterações posteriores em uma das listas não
afetam a sua cópia.
>>> A = ["Bento Gonçalves", "Campos do Jordão", "Gramado"]>>> B = list(A)>>> B.append("Ouro Preto")>>> print(B)['Bento Gonçalves', 'Campos do Jordão', 'Gramado', 'Ouro Preto']>>> print(A)['Bento Gonçalves', 'Campos do Jordão', 'Gramado']>>> id(A)139789180697672>>> id(B)139789156561992>>> id(A) == id(B)False>>> A is BFalse++. Note que as listas originais são preservadas e uma nova
lista é criada com um total de elementos igual a soma dos comprimentos das duas primeiras. Veja os exemplos abaixo digitados no Python Shell:
>>> A = ["Bento Gonçalves", "Campos do Jordão", "Gramado"]>>> B = ["Ouro Preto", "Fortaleza", "Maceió", "Rio de Janeiro"]>>> C = A + B>>> print(A)['Bento Gonçalves', 'Campos do Jordão', 'Gramado']>>> print(B)['Ouro Preto', 'Fortaleza', 'Maceió', 'Rio de Janeiro']>>> print(C)['Bento Gonçalves', 'Campos do Jordão', 'Gramado', 'Ouro Preto', 'Fortaleza', 'Maceió', 'Rio de Janeiro']>>> len(C) == len(A) + len(B) #7 == 3 + 4TrueNote que a concatenação não possui propriedade comutativa, pois a ordem dos elementos na lista de saída depende da ordem dos operandos.
>>> sabores = ["baunilha", "chocolate", "morango"] + ["napolitano", "flocos"]>>> print(sabores)['baunilha', 'chocolate', 'morango', 'napolitano', 'flocos']>>> sabores = ["napolitano", "flocos"] + ["baunilha", "chocolate", "morango"]>>> print(sabores)['napolitano', 'flocos', 'baunilha', 'chocolate', 'morango']Se as duas listas A e B possuem elementos em comum, após a concatenação, estes serão repetidos na lista produzida (veja o caso dos elementos 3, 5 e 7 no exemplo abaixo).
>>> impares = [1, 3, 5, 7, 9] #cinco primeiros números ímpares>>> primos = [2, 3, 5, 7, 11] #cinco primeiros números primos>>> uniao = impares + primos>>> print(uniao)[1, 3, 5, 7, 9, 2, 3, 5, 7, 11]
>>> sabores = ["baunilha", "chocolate", "morango"]>>> sabores = sabores + ["flocos"]>>> print(sabores)['baunilha', 'chocolate', 'morango', 'flocos']
>>> sabores = ["baunilha", "chocolate", "morango"]>>> sabores += ["flocos"]>>> print(sabores)['baunilha', 'chocolate', 'morango', 'flocos']
>>> sabores = ["baunilha", "chocolate", "morango"]>>> sabores.append("flocos")>>> print(sabores)['baunilha', 'chocolate', 'morango', 'flocos']
Apesar deles produzirem o mesmo resultado, nesse caso é
preferível utilizar o método
append(), pois
a concatenação gera uma cópia da lista toda
e a variável sabores
passa a referenciar essa nova lista criada,
sendo, portanto, uma operação mais custosa.
*
>>> [0, 1]*3 #O mesmo que: [0, 1] + [0, 1] + [0, 1][0, 1, 0, 1, 0, 1]Veja o vídeo abaixo sobre manipulação de listas em Python:
lista[início:fim]
Caso omitido, o parâmetro início é assumido como sendo 0 (zero) e o fim, quando omitido,
é assumido como sendo len(lista).
Veja os exemplos abaixo digitados no Python Shell:
>>> cidades = ['Bento Gonçalves', 'Campos do Jordão', 'Gramado', 'Ouro Preto', 'Fortaleza', 'Maceió', 'Rio de Janeiro']>>> cidades[2:6]['Gramado', 'Ouro Preto', 'Fortaleza', 'Maceió']>>> cidades[1:3]['Campos do Jordão', 'Gramado']>>> cidades[:4]['Bento Gonçalves', 'Campos do Jordão', 'Gramado', 'Ouro Preto']>>> cidades[3:]['Ouro Preto', 'Fortaleza', 'Maceió', 'Rio de Janeiro']
Por convenção do Python, o início
indica o índice do primeiro elemento que será incluído no trecho copiado,
mas o último elemento incluído no trecho é dado por
fim-1.
Ou seja, o elemento cujo índice é dado por fim
nunca é incluído no trecho copiado.
Em especial, o comando lista[:] (ou
lista[0:len(lista)])
gera uma cópia da lista toda, podendo ser usado em operações
de clonagem de uma lista, no lugar do comando
list(lista) visto anteriormente:
>>> cidades = ["Bento Gonçalves", "Campos do Jordão", "Gramado"]>>> B = cidades[:]>>> id(cidades) == id(B)False>>> B.append("Ouro Preto")>>> print(B)['Bento Gonçalves', 'Campos do Jordão', 'Gramado', 'Ouro Preto']>>> print(cidades)['Bento Gonçalves', 'Campos do Jordão', 'Gramado']del ou o método pop.del é
del lista[índice].
>>> cidades = ["Bento Gonçalves", "Campos do Jordão", "Gramado", "Ouro Preto"]>>> i = 1 #índice a ser removido>>> del cidades[i]>>> print(cidades)['Bento Gonçalves', 'Gramado', 'Ouro Preto']
A sintaxe do pop é
lista.pop(índice).
A diferença é que o pop
devolve o valor removido da lista, que pode, por exemplo, ser atribuído a uma variável.
Caso omitido o índice, o último elemento é removido.
>>> cidades = ["Bento Gonçalves", "Campos do Jordão", "Gramado", "Ouro Preto"]>>> i = 1 #índice a ser removido>>> c = cidades.pop(i)>>> print(cidades)['Bento Gonçalves', 'Gramado', 'Ouro Preto']>>> print(c)Campos do Jordão>>> c = cidades.pop()>>> print(cidades)['Bento Gonçalves', 'Gramado']>>> print(c)Ouro PretoO efeito da remoção pode também ser obtido construindo uma nova lista sem o elemento indesejado, usando fatiamento mais concatenação.
>>> cidades = ["Bento Gonçalves", "Campos do Jordão", "Gramado", "Ouro Preto"]>>> i = 1 #índice a ser removido>>> cidades = cidades[:i] + cidades[i+1:]>>> print(cidades)['Bento Gonçalves', 'Gramado', 'Ouro Preto']
Note, porém, que essa última solução é mais custosa,
por envolver a criação de uma cópia da lista toda,
sendo que a variável cidades
passará a referenciar a nova lista gerada.
Assista o vídeo abaixo, que fala sobre como os objetos são armazenados na memória e o que são as variáveis em relação a isso.
Solução:
def menorMaiorLista(lista):
maior = lista[0]
menor = lista[0]
for x in lista:
if x > maior:
maior = x
elif x < menor:
menor = x
return menor,maior
Essa função poderia
ser testada no IDLE, por exemplo, com a seguinte chamada:
m,M = menorMaiorLista([5,-4,18,8,-9,4])
print("menor =",m,", maior=",M)
def insereSeNovo(x, lista):
que devolve o índice em que o real x
ocorre em lista ou, caso x não estiver
na lista, insere x no final da lista e
devolve o índice dessa posição.
n e uma sequência de n números reais, escreva um programa (usando a função do item anterior)
que conta e imprime quantas vezes cada número ocorre na sequência.Solução 1:
def insereSeNovo(x, lista):
i = 0
achou = False
while i < len(lista) and not achou:
if lista[i] == x:
achou = True
ind = i
i += 1
if not achou:
lista.append(x)
ind = len(lista)-1
return ind
# programa principal:
def main():
n = int(input("Digite n: "))
i = 0
listaNum = []
listaCont = []
while i < n:
num = float(input("Digite num: "))
ind = insereSeNovo(num, listaNum)
if ind >= len(listaCont):
listaCont.append(0)
listaCont[ind] += 1
i += 1
i = 0
while i < len(listaNum):
print("%.2f aparece %d vezes"%(listaNum[i],listaCont[i]))
i += 1
main()
Solução 2:
Uma solução mais compacta para a função
insereSeNovo:
def insereSeNovo(x, lista):
i = 0
while i < len(lista):
if lista[i] == x:
return i
i += 1
lista.append(x)
return len(lista)-1
Solução 3:
Uma solução alternativa para a função
insereSeNovo que utiliza o comando if x not in lista:
def insereSeNovo(x, lista):
if x not in lista:
lista.append(x)
ind = len(lista)-1
else: # eu sei que x está na lista
ind = 0
while lista[ind] != x:
ind += 1
return ind
l1
e l2) e devolve True caso:
l1 e l2 tem o mesmo tamanho el1 e l2 são
todos iguais e na mesma ordem.False.n > 0 e determina se ele é ou não palíndromo usando as
funções anteriores.
Um número inteiro é palíndromo se ele
possui a mesma sequência de dígitos quando
lido tanto da direita para a esquerda como da esquerda para a direita.
Solução 1:
def listaDeDigitos(n):
lista = []
while n > 0:
dig = n%10
lista.append(dig)
n = n//10
return lista
def ordemReversa(lista):
inv = []
i = len(lista)-1
while i >= 0:
inv.append(lista[i])
i -= 1
return inv
def iguais(l1, l2):
if len(l1) != len(l2):
return False
i = 0
while i < len(l1):
if l1[i] != l2[i]:
return False
i += 1
return True
# programa principal:
def main():
n = int(input("Digite n: "))
lista = listaDeDigitos(n)
inv = ordemReversa(lista)
if iguais(lista, inv):
print(n,"é palíndromo")
else:
print(n,"não é palíndromo")
main()
Soluções alternativas:
Uma implementação alternativa para a
função ordemReversa.
Nessa versão usamos, no início do código,
o comando [0]*n
que gera uma lista com n elementos nulos.
def ordemReversa(lista):
n = len(lista)
inv = [0]*n
i = 0
while i < n:
inv[i] = lista[n-1-i]
i += 1
return inv
Python permite a comparação de listas (ex: if l1 == l2:).iguais poderia se resumir simplesmente a:
def iguais(l1, l2):
return l1 == l2
Observações:
Python permite inverter listas (in place) usando lista.reverse().
Para criar uma cópia de uma lista a
podemos usar b = list(a), ou usar b = a[:]
Logo, uma solução para o programa principal
usando esses recursos disponíveis na linguagem poderia ser:
def main():
n = int(input("Digite n: "))
lista = listaDeDigitos(n)
inv = list(lista)
inv.reverse()
if inv == lista:
print(n,"é palíndromo")
else:
print(n,"não é palíndromo")
main()
ini e fim, e uma lista L,
tal que 0 <= ini < fim <= len(L) e calcula a
soma dos elementos L[i], para ini <= i < fim.n > 0 e uma sequência com n
números reais, e determina um segmento de soma máxima.
Um segmento é uma subsequência de
números consecutivos, com pelo menos um
elemento.
Exemplo: Na sequência abaixo com n = 12
5, 2, -2, -7, 3, 14, 10, -3, 9, -6, 4, 1,
a soma do segmento de soma máxima é 3+14+10-3+9 = 33.
Solução 1:
def somasegmento(ini,fim,L):
soma = 0.0
i = ini
while i < fim:
soma += L[i]
i += 1
return soma
def main():
n = int(input("Digite n: "))
lista = []
for i in range(n):
num = float(input("Digite num: "))
lista.append(num)
smax = lista[0]
imax,fmax = 0,1
for i in range(n):
for f in range(i+1,n+1):
s = somasegmento(i,f,lista)
if s > smax:
smax = s
imax = i
fmax = f
print("Soma máxima =",lista[imax],end=" ")
for i in range(imax+1,fmax):
if(lista[i] < 0.0):
print(lista[i],end=" ")
else:
print("+",lista[i],end=" ")
print("=",smax)
main()
Solução 2:
Solução alternativa da função
somasegmento usando o laço for.
def somasegmento(ini,fim,L):
soma = 0.0
for i in range(ini, fim):
soma += L[i]
return soma
Solução 3:
Solução compacta, aproveitando os
recursos já existentes do Python de fatiamento de listas
e soma dos valores de uma lista usando a função sum (exemplo, sum([3,-2,7]) gera o valor 8).
def somasegmento(ini,fim,L):
return sum(L[ini:fim])
Veja o vídeo abaixo, do prof. Fabio Kon (IME-USP), que apresenta alguns conceitos simples e úteis, que ajudam no desenvolvimento de programas em Python.
Veja o vídeo abaixo, intitulado "Depuração com funções", do prof. Fabio Kon (IME-USP).
Para permitir isso, o Python tem uma maneira de colocar as definições em um arquivo e então usá-las em um script ou em uma execução interativa do interpretador. Tal arquivo é chamado de módulo; definições de um módulo podem ser importadas por outros módulos, por um script ou diretamente no Python Shell.
Um módulo é um arquivo contendo definições e instruções Python. O nome do arquivo é o nome do módulo acrescido do sufixo .py.
Por exemplo, use seu editor de texto favorito para criar um arquivo chamado ponto.py no diretório atual com o seguinte conteúdo:
import math
def distancia(Pa, Pb):
""" Calcula a distância entre dois pontos Pa = [xa,ya] e Pb = [xb,yb]"""
xa,ya = Pa #xa,ya = Pa[0],Pa[1]
xb,yb = Pb #xa,ya = Pb[0],Pb[1]
dx = xb-xa
dy = yb-ya
d = math.sqrt(dx*dx + dy*dy)
return d
Considerando um ponto como uma lista com dois elementos reais, correspondendo às
coordenadas x e y, o módulo ponto acima
define uma função para calcular a distância euclidiana
entre dois pontos fornecidos.
Para calcular a raiz quadrada, usamos a função
sqrt do módulo math do Python, usando a sintaxe math.sqrt.
Agora, crie um segundo arquivo chamado poligono.py no mesmo diretório com o seguinte conteúdo:
import ponto
def perimetro(Pol):
"""Calcula o perímetro de um polígono Pol = [P1, P2, ..., Pn] composto por n pontos."""
peri = 0.0 #perímetro
Pant = Pol[-1] #ponto anterior
for Pi in Pol:
dist = ponto.distancia(Pant, Pi)
peri += dist
Pant = Pi
return peri
Considerando um polígono como uma lista dos seus vértices consecutivos,
o módulo poligono acima
define uma função para calcular o perímetro de um polígono
fornecido, ou seja, a soma de todos os seus lados. Porém, como cada
vértice é o ponto comum entre os lados do polígono,
podemos calcular o tamanho de cada lado usando a função
distancia
do módulo ponto.
Para isso, precisamos primeiramente importar o módulo ponto, usando o comando import ponto.
Feito isso, podemos então chamar a função
distancia usando a sintaxe
ponto.distancia.
Agora entre no interpretador Python e importe o módulo com o seguinte comando:
>>> import poligono
poligono é importado, o interpretador procura um módulo embutido com este nome. Se não encontra, procura um arquivo chamado poligono.py em uma lista de diretórios incluídos na variável sys.path.
>>> import sys>>> print(sys.path)['', '/home/pmiranda', '/usr/bin', '/usr/lib/python35.zip', '/usr/lib/python3.5', '/usr/lib/python3.5/plat-x86_64-linux-gnu', '/usr/lib/python3.5/lib-dynload', '/home/pmiranda/.local/lib/python3.5/site-packages', '/usr/local/lib/python3.5/dist-packages', '/usr/lib/python3/dist-packages']
Se o comando import poligono
não estiver funcionando, você deve incluir o diretório que contém os arquivos poligono.py e ponto.py na lista sys.path.
No meu caso os arquivos estão no diretório do Linux /home/pmiranda/Desktop/MAC2166_1s20/modulos. Logo, podemos usar:
>>> sys.path.append('/home/pmiranda/Desktop/MAC2166_1s20/modulos')
No caso do sistema operacional Windows, a estrutura das pastas será diferente
e você deve usar um comando similar a este: sys.path.append('C:\\user\\mydir')
O comando import poligono não coloca os nomes das funções definidas em poligono diretamente na tabela de símbolos atual; isso coloca somente o nome do módulo poligono. Usando o nome do módulo você pode acessar as funções através da sintaxe nome_do_módulo.nome_da_função:
>>> poligono.perimetro([[0,0],[1,0],[1,1],[0,1]])4.0
Se pretender usar uma função muitas vezes, você pode atribui-lá a um nome local:
>>> perimetro = poligono.perimetro>>> perimetro([[0,0],[1,0],[1,1],[0,1]])4.0
importlib.reload() para recarregar o módulo:
>>> import importlib>>> importlib.reload(poligono)
Dentro de um módulo, o nome do módulo (como uma string) está disponível como o valor da variável global __name__.
>>> poligono.__name__'poligono'
Por exemplo, se você adicionar o código
print(__name__) ao final
do arquivo poligono.py,
ao importar esse módulo em um Python Shell recém-aberto teremos:
>>> import poligonopoligono
No entanto, quando você roda um módulo Python no modo script (clicando em "Run Module" tal como indicado na figura abaixo),
o código no módulo será executado, da mesma forma que quando
é importado, mas com a variável
__name__ com
valor "__main__",
ao invés de valer a string do nome do módulo
"poligono".
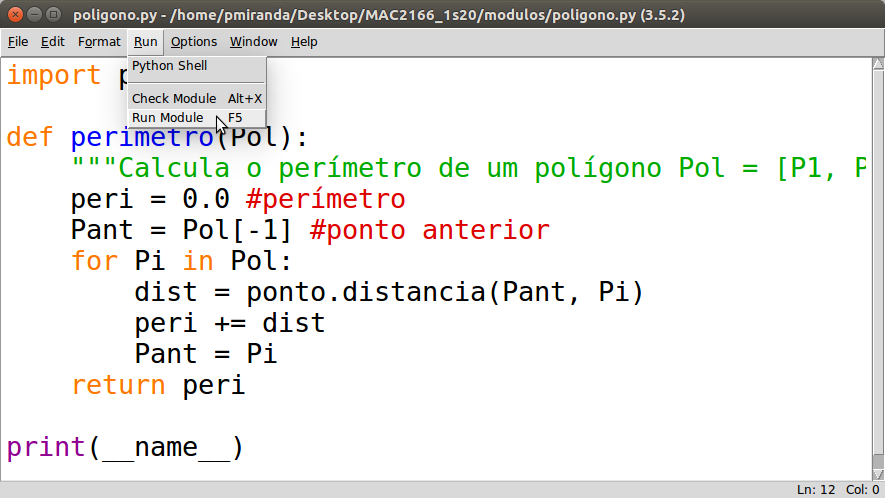
Ou seja, no Python Shell teremos como saída:

Isto significa que adicionando este código abaixo ao final do módulo
poligono (no lugar do print(__name__)):
if __name__ == "__main__":
per = perimetro([[0,0],[1,0],[1,1],[0,1]])
print("Perímetro:",per)
você pode tornar o arquivo utilizável tanto como script quanto como um módulo importável, porque o código acima só roda se o módulo é executado como arquivo "principal". Se o módulo é importado, o código não é executado.
Ou seja, se rodarmos agora o módulo poligono no modo script, teremos como saída:

Isso é frequentemente usado para fornecer uma interface de usuário conveniente para um módulo, ou para realizar testes (rodando o módulo como um script executa um conjunto de testes) para verificar a integridade do módulo.
Em muitas aplicações, precisamos processar dados bidimensionais
(gráfico cartesiano de coordenadas, imagens digitais,
matrizes de sistemas de equações lineares em Álgebra Linear).
Matriz é uma tabela organizada em linhas e colunas no formato m x n, onde m representa o número de linhas e n o número de colunas, tal como indicado na figura abaixo.

n elementos.
Por exemplo, o código abaixo cria uma matriz com três linhas e quatro colunas:
>>> A = [[4, 1, 8, 3], [2, 5, 7, 0], [6, 9, 0, 3]]ai,j é o elemento que está na linha i e coluna j, com os índices iniciando no 1.
Em Python, os índices começam no zero.
Logo, para acessar o elemento de valor 7 na matriz A definida acima, usamos i = 1
e j = 2. Para acessar um elemento da matriz na i-ésima linha e j-ésima coluna usamos a sintaxe: nome_matriz[i][j]
Exemplos:
>>> A[0][0]4>>> A[0][1]1>>> A[0][2]8>>> A[0][3]3>>> A[1][0]2>>> A[2][1]9
A i-ésima linha da matriz pode ser obtida como uma lista usando a sintaxe: nome_matriz[i]
Exemplos:
>>> A[0][4, 1, 8, 3]>>> A[1][2, 5, 7, 0]>>> A[2][6, 9, 0, 3]
len().
>>> len(A) #número de linhas3>>> len(A[0]) #número de colunas4Para criar uma matriz de dimensões arbitrárias, poderíamos pensar em usar o seguinte código:
>>> m = 3 #número de linhas>>> n = 5 #número de colunas>>> valor = 0 #valor inicial de preenchimento>>> linha = [valor]*n>>> matriz = [linha]*m>>> print(matriz)[[0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0]]
No entanto, ao modificar o valor do elemento matriz[0][0] na posição i = 0 e
j = 0 da matriz obtemos o seguinte resultado:
>>> matriz[0][0] = 1>>> print(matriz)[[1, 0, 0, 0, 0], [1, 0, 0, 0, 0], [1, 0, 0, 0, 0]]
Observe que, estranhamente, os elementos matriz[1][0] e matriz[2][0] também tiveram seus
valores alterados.
Isso ocorre porque o comando matriz = [linha]*m
gerou uma matriz em que todas linhas são, na verdade, referências
para a mesma lista na memória. Ou seja:
>>> id(matriz[0]) == id(matriz[1])True>>> id(matriz[0]) == id(matriz[2])True
Para criar uma matriz de dimensões arbitrárias corretamente,
podemos iniciar a matriz com a lista vazia []
e ir, em um laço, gradualmente adicionado suas linhas como clones da lista obtida via o comando linha = [valor]*n, tal como indicado no código abaixo:
def cria_matriz(m, n, valor):
matriz = []
linha = [valor]*n
for i in range(m):
matriz.append(linha[:])
return matriz
Podemos também criar cada uma das linhas a partir de uma lista
vazia, usando uma estrutura de laços encaixados,
tal como apresentado na solução alternativa
abaixo:
def cria_matriz(m, n, valor):
matriz = []
for i in range(m):
linha = []
for j in range(n):
linha.append(valor)
matriz.append(linha)
return matriz
Solução:
def main():
A = leia_matriz()
if simetrica(A):
print("Matriz simétrica")
else:
print("Matriz não é simétrica")
def leia_matriz():
nlinhas = int(input("Digite o número de linhas: "))
ncolunas = int(input("Digite o número de colunas: "))
matriz = []
for i in range(nlinhas):
linha = []
for j in range(ncolunas):
num = int(input("Digite elem (%d,%d): "%(i,j)))
linha.append(num)
matriz.append(linha)
return matriz
def simetrica(matriz):
nlinhas = len(matriz)
ncolunas = len(matriz[0])
if nlinhas != ncolunas:
return False
for i in range(nlinhas):
for j in range(i):
if matriz[i][j] != matriz[j][i]:
return False
return True
main()
m x n e que conta o número de linhas e colunas que têm apenas zeros.
Exemplo:
Matriz: 4 x 5
0 0 0 0 1
0 0 0 0 0
0 1 0 0 0
0 0 0 0 0
Linhas nulas = 2
Colunas nulas = 3Solução:
def leia_matriz():
m = int(input("Digite m: "))
n = int(input("Digite n: "))
matriz = []
for i in range(m):
linha = []
for j in range(n):
num = int(input("Digite elem (%d,%d): "%(i,j)))
linha.append(num)
matriz.append(linha)
return matriz
def main():
A = leia_matriz()
m = len(A)
n = len(A[0])
lin_nulas,col_nulas = 0,0
for i in range(m):
zerada = True
for j in range(n):
if A[i][j] != 0:
zerada = False
if zerada:
lin_nulas += 1
for j in range(n):
zerada = True
for i in range(m):
if A[i][j] != 0:
zerada = False
if zerada:
col_nulas += 1
print("Linhas nulas =",lin_nulas)
print("Colunas nulas =",col_nulas)
main()
Exemplo:
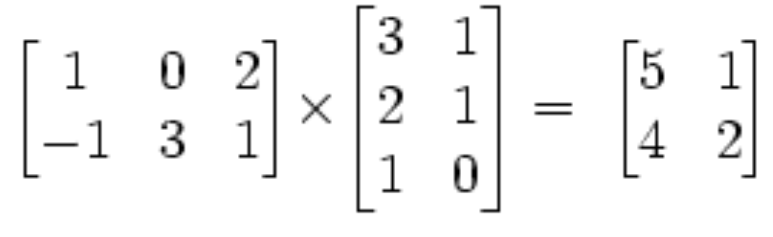
Observe que o valor 5 na matriz de saída é calculado
como 5 = 1*3 + 0*2 + 2*1.

Solução:
def cria_matriz(nlinhas, ncolunas, valor):
matriz = []
for i in range(nlinhas):
linha = []
for j in range(ncolunas):
linha.append(valor)
matriz.append(linha)
return matriz
def leia_matriz():
nlinhas = int(input("Digite o número de linhas: "))
ncolunas = int(input("Digite o número de colunas: "))
matriz = []
for i in range(nlinhas):
linha = []
for j in range(ncolunas):
num = float(input("Digite elem (%d,%d): "%(i,j)))
linha.append(num)
matriz.append(linha)
return matriz
def imprima_matriz(matriz):
nlinhas = len(matriz)
ncolunas = len(matriz[0])
print("Matriz: %d x %d"%(nlinhas,ncolunas))
for i in range(nlinhas):
for j in range(ncolunas):
print("%7.2f"%(matriz[i][j]), end="")
print()
def main():
A = leia_matriz()
B = leia_matriz()
if len(A[0]) != len(B):
print("Matrizes incompatíveis")
return
m = len(A)
n = len(A[0])
p = len(B[0])
C = cria_matriz(m, p, 0.0)
for i in range(m):
for j in range(p):
C[i][j] = 0.0
for k in range(n):
C[i][j] += A[i][k]*B[k][j]
imprima_matriz(C)
main()
Veja o vídeo abaixo sobre o exercício resolvido de multiplicação de matrizes:
Nesse jogo, o campo minado pode ser representado por uma matriz retangular. Algumas posições da matriz contém minas. Inicialmente, o conteúdo da matriz é ocultado do jogador. Cada posição pode ser revelada clicando sobre ela, e se a posição clicada contiver uma mina, então o jogo acaba. Se, por outro lado, a posição não contiver uma mina, então um número aparece, indicando a quantidade de posições adjacentes que contêm minas; O jogo é ganho quando todas as posições que não têm minas são reveladas.
Nesse exercício, você deve ciar algumas funções que podem ser utilizadas na implementação desse jogo.
(lin, col) da matriz, e conta quantas posições ao redor da posição (lin, col) contém o valor -1 (valor adotado para representar uma mina).
Por posições ao redor, considere as quatro posições
vizinhas à direita, à esquerda, em cima e em baixo,
isto é, (lin,col+1), (lin,col-1),
(lin-1,col) e (lin+1,col), e também
as quatro diagonais (lin+1,col+1), (lin-1,col-1),
(lin-1,col+1) e (lin+1,col-1), tal como indicado
na ilustração abaixo.

O uso de constantes é uma boa prática de programação. No caso do campo minado, ao invés de utilizar o valor -1, podemos criar uma constante (variável que nunca muda de valor após criada) chamada MINA com o valor -1.
Solução 1:
Consideramos uma construção de laços encaixados para
gerar as coordenadas dos elementos vizinhos da posição (lin,col).
MINA = -1
def contaMinas(campo, lin, col):
m = len(campo)
n = len(campo[0])
minas = 0
for i in range(lin-1,lin+2):
for j in range(col-1,col+2):
if i >= 0 and i < m and j >= 0 and j < n:
if i != lin or j != col: #para desconsiderar a posição central (lin,col)
if campo[i][j] == MINA:
minas += 1
return minas
Solução 2:
Guardamos os deslocamentos relativos verticais e horizontais
(di,dj) das posições dos elementos vizinhos
em relação ao elemento central
(lin,col) em duas listas
Ldi e Ldj, respectivamente.
Desse modo podemos então acessar qualquer um dos vizinhos
de (lin,col), bastando
adicionar a essa posição
o respectivo deslocamento relativo
previamente armazenado nas listas.
Por exemplo, o vizinho à direita pode ser acessado
por (lin,col) + (0,1).
Na solução abaixo, devido à ordem dos deslocamentos colocados nas
listas Ldi e Ldj, os vizinhos da posição
(lin,col) são percorridos no sentido horário,
começando pelo vizinho na posição (lin-1,col-1).
MINA = -1
def contaMinas(campo, lin, col):
Ldj = [-1, 0, 1, 1, 1, 0, -1, -1]
Ldi = [-1, -1, -1, 0, 1, 1, 1, 0]
m = len(campo)
n = len(campo[0])
minas = 0
for k in range(len(Ldj)):
i = lin + Ldi[k]
j = col + Ldj[k]
if i >= 0 and i < m and j >= 0 and j < n:
if campo[i][j] == MINA:
minas += 1
return minas
A elegância da solução acima reside no fato de que ela pode ser facilmente customizada para diferentes tipos de vizinhança, bastando editar as listas dos deslocamentos relativos.
Solução:
MINA = -1
def contaMinasCampo(campo):
m = len(campo)
n = len(campo[0])
for i in range(m):
for j in range(n):
if campo[i][j] != MINA:
campo[i][j] = contaMinas(campo, i, j)
m, n e
nminas, e que cria e devolve uma matriz m x n de 0's (posições livres) e -1's (minas),
sendo que nminas especifica a quantidade de minas
a serem colocadas em posições aleatórias da matriz.
Solução 1:
Inicialmente, uma matriz zerada com todas posições livres
é criada e, na sequência, as minas são então colocadas nas primeiras linhas da matriz da esquerda para a direita até completar o total de nminas. Depois, embaralhamos os elementos da matriz,
sorteando para cada elemento da matriz uma nova posição e procedendo com a troca.
import random
MINA = -1
LIVRE = 0
def criaMatriz(m, n, valor):
matriz = []
for i in range(m):
linha = []
for j in range(n):
linha.append(valor)
matriz.append(linha)
return matriz
def embaralha(matriz):
m = len(matriz)
n = len(matriz[0])
for i in range(m):
for j in range(n):
ii = random.randrange(0,m)
jj = random.randrange(0,n)
matriz[i][j], matriz[ii][jj] = matriz[ii][jj], matriz[i][j]
def criaCampo(m, n, nminas):
campo = criaMatriz(m, n, LIVRE)
k = 0
for i in range(m):
for j in range(n):
if k < nminas:
campo[i][j] = MINA
k += 1
embaralha(campo)
return campo
Solução 2:
Uma solução mais pythonica, utilizando recursos
já existentes no Python, pode considerar o uso da
função random.shuffle()
do módulo random para embaralhar
uma lista contendo m x n elementos, dos quais
nminas elementos são -1's (minas) e os demais são nulos.
Em seguida, basta converter a lista embaralhada para uma matriz m x n correspondente.
import random
MINA = -1
LIVRE = 0
def criaCampo(m, n, nminas):
C = [MINA]*nminas + [LIVRE]*(m*n - nminas)
random.shuffle(C)
campo = []
for i in range(m):
campo.append(C[i*n:(i+1)*n])
return campo
n x n
é um quadrado latino de ordem n se em cada linha
e em cada coluna aparecem todos os
inteiros 1,2,3,...,n (ou seja,
cada linha e coluna é
permutação dos inteiros 1,2,...,n).
Por exemplo, veja o quadrado latino abaixo.
A = [ [1,2,3],
[2,3,1],
[3,1,2] ]
(a) Escreva uma função que recebe como parâmetro uma lista L com n inteiros e verifica se em L ocorrem todos os inteiros de 1 a n.
(b) Usando a função acima, verifique se uma dada matriz
inteira A de dimensão n x n é um quadrado latino de ordem n.
def leitura_matriz(nlinhas, ncolunas):
M = []
for i in range(nlinhas):
linha = []
for j in range(ncolunas):
valor = int(input("(%d,%d):"%(i,j)))
linha.append(valor)
M.append(linha)
return M
def lista_latina(L):
for i in range(1,len(L)+1,1):
if i not in L:
return False
return True
def main():
n = int(input("Digite n: "))
A = leitura_matriz(n, n)
latino = True
#Testa linhas:
for i in range(len(A)):
if not lista_latina(A[i]):
latino = False
#Testa colunas:
for j in range(len(A[0])):
C = []
for i in range(len(A)):
C.append(A[i][j])
if not lista_latina(C):
latino = False
if latino:
print("Quadrado latino")
else:
print("Não é quadrado latino")
main()
Por exemplo, a matriz abaixo é um quadrado mágico.
A = [ [8, 0, 7],
[4, 5, 6],
[3, 10, 2] ]
Dada uma matriz quadrada A de dimensão n x n, verificar se A é um quadrado mágico.
Solução 1:
Testa a soma das linhas, colunas e diagonais
em laços separados.
Para a soma das linhas usa a função
sum() disponível no Python
que gera a soma dos elementos de uma lista fornecida.
def leitura_matriz(nlinhas, ncolunas):
M = []
for i in range(nlinhas):
linha = []
for j in range(ncolunas):
valor = int(input("(%d,%d):"%(i,j)))
linha.append(valor)
M.append(linha)
return M
def main():
n = int(input("Digite n: "))
A = leitura_matriz(n, n)
magico = True
soma_esperada = sum(A[0])
#Testa linhas:
for i in range(1,len(A)):
if sum(A[i]) != soma_esperada:
magico = False
#Testa colunas:
for j in range(len(A[0])):
soma = 0
for i in range(len(A)):
soma += A[i][j]
if soma != soma_esperada:
magico = False
#Diagonal principal:
soma = 0
for i in range(len(A)):
soma += A[i][i]
if soma != soma_esperada:
magico = False
#Diagonal secundária:
soma = 0
j = n-1
for i in range(len(A)):
soma += A[i][j]
j -= 1
if soma != soma_esperada:
magico = False
if magico:
print("Quadrado mágico")
else:
print("Não é quadrado mágico")
main()
Solução 2:
Usa uma lista soma_linhas para armazenar a soma de cada linha e
uma lista soma_colunas para a soma das colunas.
Ou seja, no final, soma_linhas[i] armazenará a soma dos elementos da i-ésima linha e soma_colunas[j] a soma dos elementos da j-ésima coluna. Todas as somas de linhas, colunas e diagonais são então calculadas dentro da mesma estrutura de laços encaixados.
def leitura_matriz(nlinhas, ncolunas):
M = []
for i in range(nlinhas):
linha = []
for j in range(ncolunas):
valor = int(input("(%d,%d):"%(i,j)))
linha.append(valor)
M.append(linha)
return M
def main():
n = int(input("Digite n: "))
A = leitura_matriz(n, n)
magico = True
soma_linhas = [0]*n
soma_colunas = [0]*n
soma_diag_pri = 0
soma_diag_sec = 0
for i in range(n):
for j in range(n):
soma_linhas[i] += A[i][j]
soma_colunas[j] += A[i][j]
if i == j:
soma_diag_pri += A[i][j]
if i+j == n-1:
soma_diag_sec += A[i][j]
soma_esperada = soma_diag_pri
if soma_esperada != soma_diag_sec:
magico = False
for i in range(n):
if soma_linhas[i] != soma_esperada:
magico = False
if soma_colunas[i] != soma_esperada:
magico = False
if magico:
print("Quadrado mágico")
else:
print("Não é quadrado mágico")
main()
str, função len).upper, lower, capitalize, strip, count, replace, center, find).ord e chr).split().
Um string (= tipo str) é uma sequência de caracteres.
Por ser uma sequência de caracteres, podemos fazer uma analogia de strings com listas em Python. Assim como elementos de listas, um caractere de um string pode ser acessado por meio de um índice, o comprimento pode ser dado pela função len(), e os caracteres podem ser fatiados e concatenados.
Veja os exemplos abaixo:
>>> texto = "Devagar se chega ao longe">>> len(texto)25>>> texto[0]'D'>>> texto[8]'s'>>> texto[11:16]'chega'>>> texto[20:]'longe'A grande diferença em relação às listas (que são dados mutáveis) é que strings em Python são imutáveis, ou seja, não é possível alterar seus elementos. Veja os exemplos abaixo:
>>> nome = "Paulo">>> nome[4] = 'a'Traceback (most recent call last): File "<pyshell#12>", line 1, in <module> nome[4] = 'a'TypeError: 'str' object does not support item assignment
>>> nome = "Paulo">>> nome.append(" Miranda")Traceback (most recent call last): File "<pyshell#13>", line 1, in nome.append(" Miranda")AttributeError: 'str' object has no attribute 'append'Para gerar modificações em um texto fornecido em Python, é necessário criar um novo string. Para isso, podemos gerar novos strings usando o operador de concatenação e o comando de fatiamento. O operador de concatenação gera um novo texto com conteúdo igual à fusão dos dois textos fornecidos. O comando de fatiamento gera cópias de trechos específicos extraídos do texto fornecido. Veja os exemplos abaixo:
>>> nome = "Paulo">>> nome = nome[:len(nome)-1] + 'a'>>> print(nome)Paula
>>> nome = "Paulo">>> nome = nome + " Miranda">>> print(nome)Paulo MirandaComo vimos na primeira aula deste curso, tudo o que um computador armazena e processa são números (internamente no sistema binário). Para que possam ser processados pelo computador, precisamos representar os caracteres por meio de números.
Existem diferentes codificações (= representações numéricas) que podem ser usadas para caracteres. Algumas codificações são específicas para uma língua (como Chinês, Russo, etc.), enquanto outras podem ser usadas para múltiplas línguas. Um mesmo caractere pode aparecer em diferentes codificações. Entretanto, duas codificações diferentes podem usar códigos numéricos diferentes para representar um mesmo caractere, gerando problemas de incompatibilidade. Para solucionar esses problemas e prover uma representação unificada dos alfabetos de todas as línguas da humanidade, o padrão Unicode foi desenvolvido. O Unicode fornece um número único para cada caractere, independentemente da plataforma ou programa.
Na versão 3.X do Python, strings são armazenadas no padrão Unicode em uma instância do tipo str.
Para obter o código Unicode de um caractere, como um inteiro, podemos usar a função ord() do Python.
Já o caminho inverso pode ser feito usando a função
chr(). Veja os exemplos abaixo:
>>> ord('a')97>>> ord('b')98>>> ord('c')99>>> ord('z')122>>> ord('8')56>>> ord('9')57>>> ord('?')63>>> chr(97)'a'>>> chr(122)'z'>>> chr(56)'8'>>> chr(63)'?'
unicode é
usado para expressar cadeias Unicode, enquanto instâncias do tipo
str
são representações de byte.
Uma das codificações mais conhecida é a ASCII (American Standard Code for Information Interchange), que foi definida como um padrão em 1968. A ASCII foi criada para representar caracteres da língua inglesa. No ASCII os caracteres numerados de 0 a 31 são considerados de controle, e os de 32 a 127 correspondem aos caracteres comuns de um teclado de computador em inglês, incluindo letras, dígitos decimais e sinais de pontuação. Como um código ASCII é um número entre 0 e 127, ele pode ser armazenado usando-se apenas 7 bits, ou seja, ele cabe dentro de um byte (= 8 bits). A numeração da tabela Unicode é compatível com a tabela ASCII. Logo, podemos executar o seguinte programa para ver os caracteres de 32 a 127 da tabela ASCII:
print("Tabela ASCII de 32 a 127: ")
for i in range(32, 128, 3):
print("ASCII[ %3d ] = '%s' | ASCII[ %3d ] = '%s' | ASCII[ %3d ] = '%s'"%
(i, chr(i), i+1, chr(i+1), i+2, chr(i+2)))
Infelizmente, o alfabeto ASCII não é suficiente para escrever texto em português, pois não contém vogais com acentos e o til (ex: á, ã, é, etc.) e não possui a cedilha que se coloca sob a letra c (produzindo ç).
Para lidar com esse problema, nos anos 80 várias extensões do ASCII foram criadas usando os valores entre 128 e 255 como códigos para caracteres acentuados, resultando em códigos de 1 byte. Um exemplo de uma dessas extensões, usada para a língua portuguesa, é a codificação ISO-8859-1, também chamada de Latin1.
Os 256 primeiros códigos Unicode são idênticos aos do padrão ISO-8859-1 de forma que para exibir os demais caracteres ocidentais com acentos no Python 3.X basta imprimir também os caracteres no intervalo de 160 a 255:
print("Tabela ISO-8859-1 (Latin1) de 160 a 255: ")
for i in range(160, 256, 3):
print("Latin1[ %3d ] = '%s' | Latin1[ %3d ] = '%s' | Latin1[ %3d ] = '%s'"%
(i, chr(i), i+1, chr(i+1), i+2, chr(i+2)))
chr() para fazer a conversão do código inteiro para string.
Em geral, entretanto, esses números são escritos em notação hexadecimal (base 16). Além disso, usualmente os code points são apresentados incluindo o prefixo U+ a cada número.
Por exemplo, considere a tabela abaixo que mostra os códigos Unicode de alguns caracteres do alfabeto grego:
| número Unicode | caractere | Descrição |
|---|---|---|
| U+03B1 | α | Alpha |
| U+03B2 | β | Beta |
| U+03B3 | γ | Gamma |
| U+03B4 | δ | Delta |
| U+03B5 | ε | Epsilon |
| U+03B6 | ζ | Zeta |
| U+03B7 | η | Eta |
| U+03B8 | θ | Theta |
Por exemplo, para imprimir a letra beta, podemos usar o seguinte código:
>>> beta = chr(0x03B2)>>> print(beta)βEm Python 3.X, podemos também usar a seguinte solução alternativa:
>>> beta = "\u03B2">>> print(beta)βObservação: Por questões de simplicidade, assuma o padrão ASCII e ignore vogais acentuadas, tais como à, á, ã, etc.
Exemplo: Para o texto "Paulo" temos a seguinte saída do programa.
Digite um texto: Paulo Frequência rel. = 3/5 = 0.600000
Solução 1:
Ao invés de testar cada vogal
com uma condição correspondente sendo
explicitamente escrita (ex: if letra == 'a' or letra == 'e' or ... or letra == 'u':), na solução abaixo consideramos uma string contendo todas possíveis vogais, de modo que podemos então usar o teste mais simples if letra in vogais:.
def main():
texto = input("Digite um texto: ")
vogais = "aeiouAEIOU"
n = len(texto)
nv = 0 #número de vogais no texto.
for letra in texto:
if letra in vogais:
nv += 1
print("Frequência rel. = %d/%d = %f"%(nv,n,nv/n))
main()
Solução 2:
Solução um pouco mais complexa,
utilizando laços encaixados com as
variáveis de controle i e
j correspondendo aos
índices das strings texto e
vogais, respectivamente.
def main():
texto = input("Digite um texto: ")
vogais = "aeiouAEIOU"
n = len(texto)
nv = 0 #número de vogais no texto.
for i in range(n):
for j in range(len(vogais)):
if texto[i] == vogais[j]:
nv += 1
print("Frequência rel. = %d/%d = %f"%(nv,n,nv/n))
main()
Solução 1:
Nesta primeira solução, por questões de simplicidade, estamos assumindo o padrão ASCII e ignorando acentos, tais como à, á, ã, etc.
def maiuscula(c):
if c >= 'a' and c <='z':
c = chr(ord(c) - ord('a') + ord('A'))
return c
def main():
texto = input("Digite um texto: ")
novo = ""
for l in texto:
novo += maiuscula(l)
print(novo)
main()
Solução 2:
Uma solução mais pythonica e geral, utilizando recursos
já existentes no Python, pode considerar o uso do
método upper().
def main():
texto = input("Digite um texto: ")
print(texto.upper())
main()
separa, que recebe um string texto e um caractere separador sep. A função "corta" o texto nos separadores, retornando uma lista com as partes recortadas do texto.
Exemplo: para o texto "Nome completo;NUSP;e-mail" e sep=";" a saída deve ser a lista ['Nome completo', 'NUSP', 'e-mail'].
Solução:
def separa(texto, sep = " "):
L = []
palavra = ""
for l in texto:
if l != sep:
palavra += l
elif palavra != "":
L.append(palavra)
palavra = ""
if palavra != "":
L.append(palavra)
return L
Abaixo temos um exemplo de programa principal, que chama
a função acima para obter a lista de palavras
separadas por espaços em branco de uma linha de texto.
def main():
texto = input("Digite um texto: ")
P = separa(texto, " ")
print(P)
main()
Note, porém, que as strings no Python
já possuem um método nativo chamado split(),
que desempenha esse papel de quebrar o texto no separador fornecido.
Caso omitido, o separador é assumido como sendo o espaço em branco.
def main():
texto = input("Digite um texto: ")
P = texto.split()
print(P)
main()
Exemplo:
Digite uma frase: Pedro Álvares Cabral Comprimento da palavra mais longa é 7
Solução 1:
Uma primeira solução analisando letra por letra do texto,
sem o uso do split() para separar as palavras do texto.
def main():
frase = input("Digite uma frase: ")
tam = 0
maxtam = 0
for letra in frase:
if letra != ' ':
tam += 1
else:
tam = 0
if tam > maxtam:
maxtam = tam
print("Comprimento da palavra mais longa é",maxtam)
main()
Solução 2:
Uma segunda solução com a
separação explícita das palavras do texto,
via o método split().
def main():
frase = input("Digite uma frase: ")
palavras = frase.split()
maxtam = 0
for pal in palavras:
if len(pal) > maxtam:
maxtam = len(pal)
print("Comprimento da palavra mais longa é",maxtam)
main()
A ordenação de elementos em uma lista é uma atividade fundamental em vários problemas computacionais. De forma geral, o problema pode ser definido como:
Dado uma lista seq com N elementos, rearranjar os elementos de seq de tal modo que eles fiquem em ordem crescente, ou seja, seq[0] <= seq[1] <= ... <= seq[N-1].
Escreva uma função crescente(seq) que recebe uma lista seq e retorna True caso seq esteja em ordem crescente, e False caso contrário.
Use essa função nos demais exercícios para testar os seus próprios algoritmos de ordenação.
Solução:
def crescente(seq):
for i in range(1,len(seq)):
if seq[i] < seq[i-1]:
return False
return True
Um dos algoritmos mais simples para a ordenação de listas é a ordenação por inserção. Ele é o algoritmo naturalmente usado para ordenar um baralho de cartas. A ideia dele é a seguinte:
- Assuma que a primeira posição da lista seq (1a carta do baralho) está ordenada;
- novo = 2
- sabemos que todos os elementos anteriores ao elemento novo estão ordenados
- insira o elemento novo (seq[novo]) na posição adequada na sub lista seq[0:novo], e desloque os demais elementos, para obter a lista ordenada até o elemento novo.
- incremente novo e repita a partir do passo 3 até o último elemento da lista
Para entender esse algoritmo assista a animação desse método com dança folclórica romena ou o vídeo Insertion Sort.
Escreva a função ordenacao_insercao(seq) que recebe como parâmetro uma lista seq e a ordena usando o algoritmo de ordenação por inserção.
Uma característica importante para a eficiência de um algoritmo de ordenação é a capacidade de utilizar a mesma lista de entrada, rearranjando os elementos ao invés de criar uma nova lista ordenada.
Faça isso na sua função.
Solução:
def ordenacao_insercao(seq):
n = len(seq)
for i in range(0,n-1):
# Insere seq[i+1] em seq[0],...,seq[i].
x = seq[i+1]
j = i
while j >= 0 and seq[j] > x:
seq[j+1] = seq[j]
j -= 1
seq[j+1] = x
O algoritmo de seleção utiliza a seguinte estratégia para ordenar uma lista seq com N elementos:
- Repita com pos variando de N-1 até 0:
- acha o índice k do maior elemento na sub lista seq[0:pos+1]
- troca o elemento seq[k] com seq[pos]
- nesse instante temos que a sub lista seq[pos:] está ordenada.
Para entender esse algoritmo assista a animação desse método com dança cigana ou o vídeo Selection Sort.
Escreva a função ordenacao_selecao(seq) que recebe como parâmetro uma lista seq e a ordena usando o algoritmo de ordenação por seleção.
Assim como na função do Problema 2, você deve rearranjar os elementos da lista de entrada ao invés de criar uma nova lista ordenada.
Solução:
A solução aqui apresentada utiliza a função
auxiliar abaixo que devolve o índice do maior elemento da
lista compreendido entre os índices de 0 a n-1.
def indice_maior(seq, n):
imax = 0
for i in range(1,n):
if seq[i] > seq[imax]:
imax = i
return imax
Também utilizaremos a seguinte função auxiliar
para realizar a troca entre os elementos da lista seq
nos índices i e j:
def troca(seq, i, j):
tmp = seq[i] #Guarda cópia de backup do valor L[i] em tmp.
seq[i] = seq[j]
seq[j] = tmp
No algoritmo abaixo, a cada passo o maior elemento da lista de n elementos
é encontrado, e colocado na sua posição final definitiva
de índice n-1 no final da lista.
O processo se repete para o trecho da lista remanescente,
composto pelos primeiros n-1 elementos ainda não ordenados
(do índice zero até n-2),
e assim por diante para subtrechos cada vez menores, até ter toda a lista ordenada.
def ordenacao_selecao(seq):
"""Ordenação por seleção:
A cada passo o maior elemento da lista é
encontrado e colocado na sua posição
final definitiva. O processo se repete para o
trecho da lista remanescente."""
n = len(seq)
for tam in range(n, 1, -1):
imax = indice_maior(seq, tam)
troca(seq, imax, tam-1)
O algoritmo da bolha utiliza a seguinte estratégia para ordenar uma lista seq com N elementos:
- Repita N-1 vezes:
- varra a lista com pos variando de 1 até N-1:
- se seq[pos] for menor que o elemento anterior então:
- troca o elemento em pos com o seu anterior
A ideia é que, a cada varrida, elementos “grandes” são arrastados para a direita e elementos “pequenos” são arrastados para a esquerda da lista. Repetindo-se essas trocas por um número suficiente de vezes, obtemos a lista ordenado. No entanto, em muitos casos, é possível que a lista fique ordenada após algumas poucas trocas. Nesse caso, é possível melhorar esse algoritmo para que pare assim que se descubra que ele se tornou ordenado.
houve_troca = True
- enquanto houve_troca:
houve_troca = False
- varra a lista com pos variando de 1 até N-1:
- se seq[pos] for menor que o elemento anterior então:
- troca o elemento em pos com o seu anterior
- houve_troca = True
Para entender esse algoritmo assista a animação desse método com dança folclórica húngara ou o vídeo Bubble Sort.
Escreva a função ordenacao_bolha(seq) que recebe como parâmetro uma lista seq e a ordena usando o algoritmo de ordenação por bolha.
Assim como na função dos Problemas 2 e 3, você deve rearranjar os elementos da lista de entrada ao invés de criar uma nova lista ordenada.
Solução 1:
O laço mais interno percorre a lista
em j
comparando elementos consecutivos da lista (seq[j] e
seq[j+1]) e trocando a sua ordem sempre que
eles estiverem fora de ordem, isto é seq[j] > seq[j+1].
Após a primeira varredura, o maior elemento da lista
vai ocupar a última posição da lista,
ou seja sua posição final definitiva na lista ordenada.
A medida que os maiores valores são movidos
para o final da lista, temos a correspondente redução
do subtrecho remanescente a ser ordenado, até que
todo a lista esteja ordenada.
def ordenacao_bolha(seq):
n = len(seq)
for i in range(n-1, 0, -1):
for j in range(0,i):
if seq[j] > seq[j+1]:
troca(seq, j, j+1)
Solução 2:
Uma segunda versão do algoritmo bubble sort é apresentada abaixo. Essa variante possui um segundo critério de parada do laço. Sempre que a lista é percorrida no laço mais interno, sem que haja trocas de elementos, podemos concluir que a lista já se encontra ordenada e podemos interromper o processo.
def ordenacao_bolha(seq):
n = len(seq)
for i in range(n-1,0,-1):
houvetroca = False
for j in range(0,i):
if seq[j] > seq[j+1]:
troca(seq, j, j+1)
houvetroca = True
if not houvetroca:
break
Observação:
A método sort() da classe list disponível no Python faz ordenação:
>>> L = [8,3,7,1,2]>>> L.sort()>>> print(L)[1, 2, 3, 7, 8]
n > 0 observações
x1, x2, ..., xn, em uma lista com n elementos
da classe float, faça uma função para
calcular a sua mediana.
Mediana é o valor que separa a metade maior e a metade menor das
observações.
Por exemplo, no conjunto de dados {1, 3, 3, 5, 7, 8, 9},
a mediana é 5.
Se houver um número par de observações,
não há um único valor do meio.
Então, a mediana é definida como a média
dos dois valores do meio. Por exemplo,
no conjunto de dados {3, 5, 7, 9}, a mediana
é (5+7)/2=6.
Solução 1:
Ordenamos uma cópia da lista para encontrar o elemento central, sem alterar a lista original fornecida.
def mediana(L):
C = L[:]
C.sort()
if len(L)%2 != 0:
m = len(L)//2
return C[m]
else:
m = len(L)//2
return (C[m-1]+C[m])/2.0
Solução 2:
Podemos simplesmente usar a função statistics.median()
do módulo statistics.
>>> import statistics>>> statistics.median([1,2])1.5>>> statistics.median([1,8,2])2
open() e método close().read(), readline().for linha in arquivo:.write().Nos exercícios que fizemos no curso até a aula de hoje, sempre criamos programas que manipulavam dados digitados pelos usuários. Entretanto, essa não é a unica forma de entrada de dados que podemos usar em um programa. Uma outra forma de entrada de dados usada com frequência em programas é a leitura de dados gravados em um arquivo.
Para abrir um arquivo para leitura, podemos usar a função open(), passando como parâmetros para ela o nome (com caminho, se necessário) do arquivo a ser aberto e a string 'r' (de read, para indicar que o arquivo será aberto para leitura). A função devolve um objeto do tipo file.
Para ler o conteúdo inteiro de um arquivo var_arquivo já aberto para leitura, podemos usar a função var_arquivo.read(), que devolve uma string (str).
Depois que o uso de um arquivo já tiver sido encerrado, é preciso fechar o arquivo por meio da função close().
Veja o exemplo a seguir, que abre um arquivo chamado 'meu_arquivo.txt', lê cada o seu contéudo e o imprime.
nome_do_arquivo = "meu_arquivo.txt"
arquivo = open(nome_do_arquivo, 'r') # abre o arquivo para leitura
print("Conteúdo do arquivo '%s'\n" %nome_do_arquivo)
conteudo = arquivo.read() # lê o conteúdo do arquivo
print(conteudo)
arquivo.close() # depois do uso, fecha o arquivo
A saída do programa é a mostrada abaixo:
Para ser grande, sê inteiro: nada
Teu exagera ou exclui.
Sê todo em cada coisa. Põe quanto és
No mínimo que fazes.
Assim em cada lago a lua toda
Brilha, porque alta vive.
Ricardo Reis, 14-2-1933
(heterônimo de Fernando Pessoa)
Quando o arquivo é muito grande, ler o seu conteúdo inteiro de uma só vez não é uma boa ideia, pois ele pode ocupar toda a memória do computador. Nesse caso, o melhor é ler uma linha do arquivo por vez.
Para ler uma linha de um arquivo var_arquivo já aberto para leitura, podemos usar a função var_arquivo.readline(), que também devolve uma string (str). Quando se está no final do arquivo, a função readline() devolve uma string vazia ('').
nome_do_arquivo = "meu_arquivo.txt"
arquivo = open(nome_do_arquivo, 'r') # abre o arquivo para leitura
print("Conteúdo do arquivo '%s'\n" %nome_do_arquivo)
linha = arquivo.readline() # lê uma linha do arquivo
while linha != "": # enquanto não chegou ao final do arquivo
print(linha,end="") # imprime a linha
linha = arquivo.readline() # lê uma nova linha do arquivo
arquivo.close() # depois do uso, fecha o arquivo
A saída desse programa é igual à saída do programa anterior.
Para fazer um laço que lê todas as linhas de um arquivo (uma por vez), também podemos usar o comando for var_linha in arquivo:, onde var_linha é o nome da variável que armazenará o conteúdo de uma linha e var_arquivo é o arquivo já aberto para leitura, como ilustrado abaixo:
nome_do_arquivo = "meu_arquivo.txt"
arquivo = open(nome_do_arquivo, 'r') # abre o arquivo para leitura
print("Conteúdo do arquivo '%s'\n" %nome_do_arquivo)
for linha in arquivo: # percorre cada linha do arquivo
print(linha,end="") # imprime a linha
arquivo.close() # depois do uso, fecha o arquivo
A saída desse programa é igual à saída do programa anterior.
É possível evitar de ter que fechar explicitamente um arquivo (com close()) usando o comando with (...) as <nome_var> : na sua abertura, como no exemplo abaixo. Ao final do corpo do with, o comando with fecha automaticamente o arquivo.
nome_do_arquivo = "meu_arquivo.txt"
with open(nome_do_arquivo, 'r') as arquivo: # abre o arquivo para leitura
# Corpo do WITH
print("Conteúdo do arquivo '%s'\n" %nome_do_arquivo)
for linha in arquivo: # percorre cada linha do arquivo
print(linha,end="") # imprime a linha
print("Fim!")
Importante: Para poder reler a partir da primeira linha um arquivo que está aberto e já foi lido, é preciso reabri-lo com a função open(). Todo arquivo aberto tem um marcador que indica a posição do primeiro caracter que ainda não foi lido do arquivo (ou seja, a posição de início da próxima leitura a ser realizada). A função open() põe o marcador no início do arquivo. E a cada vez que chamamos a função read() ou a função readline(), o marcador se move para o caractere que vem em seguida do último caractere retornado. No caso de readline, o marcador se move para o primeiro caractere da próxima linha. No caso de read, o marcador se move para o final do arquivo.
Também podemos usar a função open() para criar um arquivo para a gravação de dados, passando como parâmetros para ela o nome (com caminho, se necessário) do arquivo a ser criado e a string 'w' (de write, para indicar que o arquivo será aberto para escrita).
Para gravar uma string em um arquivo var_arquivo já aberto para escrita, podemos usar a função var_arquivo.write().
Assim como na leitura de arquivos, depois que o uso de um arquivo aberto para escrita já tiver sido encerrado, é preciso fechar o arquivo por meio da função close().
Veja o exemplo a seguir, que cria um arquivo chamado 'meu_poema.txt' e grava um poema nele.
nome_do_arquivo = "meu_poema.txt"
arquivo = open(nome_do_arquivo, 'w') # Cria ou abre o arquivo para escrita
poeminha = ["Batatinha quando nasce","Espalha a rama pelo chão","Menininha quando dorme"]
for linha in poeminha:
arquivo.write(linha) # grava uma linha do poema no arquivo
arquivo.write('\n') # coloca uma quebra de linha no final da linha do poema
arquivo.close() # depois do uso, fecha o arquivo
Quando abrimos um arquivo com a opção de escrita 'w', se o arquivo não existe previamente, ele será criado pela função open(). Entretanto, caso o arquivo já exista, o seu conteúdo atual será sobreescrito (ou seja, perdido).
Para acrescentarmos conteúdo no final de um arquivo que já existe, podemos abrir o arquivo com a função open() passando como parâmetros para ela o nome (com caminho, se necessário) do arquivo a ser aberto e a string 'a' (de append, para indicar que o arquivo será aberto para escrita preservando o seu conteúdo atual). Caso o arquivo que se tenta abrir com opção 'a' não existe previamente, ele será criado pela função open().
Para gravar uma string no final de um arquivo aberto com a opção 'a', também usamos a função write().
Veja o exemplo a seguir, que adiciona novas frases ao final do arquivo chamado 'meu_poema.txt':
nome_do_arquivo = "meu_poema.txt" arquivo = open(nome_do_arquivo, 'a') # Abre o arquivo para append (acréscimo) fim_poeminha = "Põe a mão no coração" arquivo.write(fim_poeminha) arquivo.close() # depois do uso, fecha o arquivo
Faça um programa em Python que leia uma planilha no formato CSV, onde o caracter separador é o ponto e vírgula (;), em uma matriz (lista de listas) e que gere um novo arquivo no formato CSV contendo a planilha ordenada pelo seu primeiro campo.
Exemplo: Para o arquivo CSV mostrado abaixo

o programa deve obter a seguinte matriz:
[['Paulo', '8.8', '5.7', '8.2'], ['Tiago', '5.4', '6.9', '10.0'], ['Luna', '5.0', '4.3', '5.7']]
A matriz ordenada pelo seu primeiro campo fica:
[['Luna', '5.0', '4.3', '5.7'], ['Paulo', '8.8', '5.7', '8.2'], ['Tiago', '5.4', '6.9', '10.0']]
Portanto, o programa deve gerar o seguinte arquivo de saída:

Obs.: Arquivos no formato CSV são reconhecidos pelo OpenOffice/LibreOffice e programas similares. Abaixo, mostramos o arquivo gerado sendo aberto no LibreOffice:
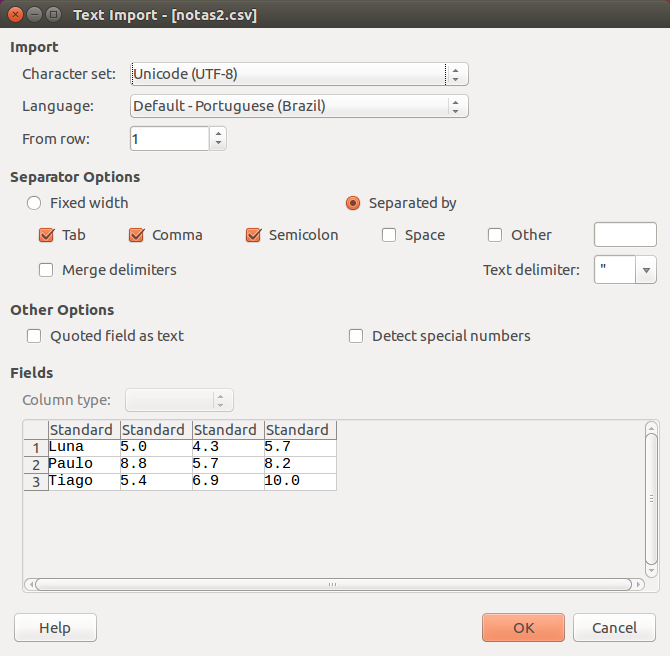
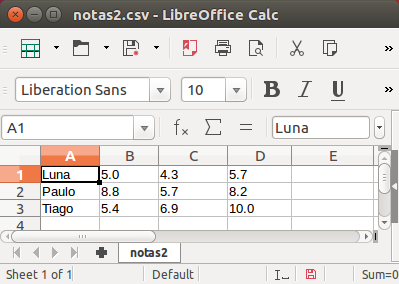
def ordenacao(M):
n = len(M)
for n in range(len(M),1,-1):
imax = 0
for i in range(1,n):
if M[i][0] > M[imax][0]:
imax = i
tmp = M[n-1]
M[n-1] = M[imax]
M[imax] = tmp
def main():
#Leitura do arquivo de entrada
arquivo = open("notas.csv", 'r')
matriz = []
for linha in arquivo:
l = linha.strip()
if len(l) > 0:
palavras = l.split(";")
matriz.append(palavras)
arquivo.close()
ordenacao(matriz)
#Gravação do arquivo de saída
arquivo = open("notas2.csv", 'w')
n = len(matriz)
m = len(matriz[0])
for i in range(n):
for j in range(m-1):
arquivo.write(matriz[i][j])
arquivo.write(";")
arquivo.write(matriz[i][m-1])
arquivo.write("\n")
arquivo.close()
main()
Inicialmente, usamos a função open() para
abrir o arquivo de nome notas.csv para leitura, tal como indicado pelo
valor 'r' (do inglês read) do segundo parâmetro de open("notas.csv", 'r'). O arquivo notas.csv deve estar no mesmo diretório do programa sendo executado,
caso contrário devemos indicar explicitamente o caminho completo (path) do arquivo.
O comando for linha in arquivo: é então usado para
processar as linhas do arquivo, como se ele fosse uma lista de strings contendo as linhas do arquivo. Usamos o método strip() para eliminar o '\n' e demais caracteres considerados "brancos" (como o espaço e o tab) no início e final das linhas.
Adicionamos então na matriz as linhas não vazias do aquivo, como uma lista de palavras separadas por ; utilizando o método split(";").
Usamos então close para fechar o arquivo.
A matriz ordenada é então gravada no disco. Para isso,
abrimos o arquivo de saída notas2.csv no modo gravação,
tal como indicado pelo valor 'w' (do inglês write) do segundo parâmetro
do comando open("notas2.csv", 'w').
O arquivo notas2.csv é gerado no mesmo diretório do programa sendo executado,
caso contrário devemos incluir todo o caminho (path) no seu nome.
Os elementos da matriz são gravados no disco usando
o método write(). Dado que o comando write()
não inclui automaticamente o caracter de quebra de linha,
devemos usar o "\n" explicitamente quando necessário.
n > 0, faça uma
função molduras_concentricas(n, v1, v2) que gera
uma matriz quadrada nxn preenchida
com um padrão de molduras concêntricas, alternando entre
os dois valores fornecidos (v1 e v2) e iniciando com o valor v1 na
posição central da matriz,
tal como apresentado nos exemplos abaixo.
Para n=5, v1=0, v2=1:
[[0, 0, 0, 0, 0], [0, 1, 1, 1, 0], [0, 1, 0, 1, 0], [0, 1, 1, 1, 0], [0, 0, 0, 0, 0]]
Para n=7, v1=0, v2=1:
[[1, 1, 1, 1, 1, 1, 1], [1, 0, 0, 0, 0, 0, 1], [1, 0, 1, 1, 1, 0, 1], [1, 0, 1, 0, 1, 0, 1], [1, 0, 1, 1, 1, 0, 1], [1, 0, 0, 0, 0, 0, 1], [1, 1, 1, 1, 1, 1, 1]]
Para n=15, v1=0, v2=1:
[[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1], [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1], [1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1], [1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1], [1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1], [1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1], [1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1], [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]]
Solução:
#Cria matriz com m linhas e n colunas
def cria_matriz(m, n, valor):
M = []
for i in range(m):
linha = []
for j in range(n):
linha.append(valor)
M.append(linha)
return M
def molduras_concentricas(n, v1, v2):
M = cria_matriz(n, n, 0)
for i in range(n):
for j in range(n):
#dh = distancia horizontal ao centro
dh = n//2 - j
if dh < 0:
dh = -dh
#dv = distancia vertical ao centro
dv = n//2 - i
if dv < 0:
dv = -dv
if dh > dv:
if dh % 2 == 0:
M[i][j] = v1
else:
M[i][j] = v2
else:
if dv % 2 == 0:
M[i][j] = v1
else:
M[i][j] = v2
return M
Exemplo: Para n = 101, a seguinte imagem deve ser gerada pelo programa

def grava_PGM(M):
arquivo = open("fig01.pgm", 'w')
arquivo.write("P2\n")
m = len(M)
n = len(M[0])
arquivo.write("%d %d\n"%(n,m))
arquivo.write("255\n")
for i in range(m):
for j in range(n):
arquivo.write(" %3d"%(M[i][j]))
arquivo.write("\n")
arquivo.close()
def main():
n = int(input("Digite n: "))
M = molduras_concentricas(n, 0, 255)
grava_PGM(M)
main()
Obs.: Invertendo o conteúdo das variáveis v1 e v2, obtemos uma imagem com o brilho invertido. Podemos gerar a gif animada abaixo, gravando essa segunda imagem em um arquivo fig02.pgm e usando o conversor de imagens do ImageMagick, executando no terminal o comando: convert -delay 10 *.pgm out.gif

A gif animada acima foi gerada usando n=101.
Que modificação você poderia fazer no código para obter molduras mais grossas como na figura abaixo?

Veja a videoaula do prof. Fabio Kon (IME-USP) sobre Recursão:
Uma função é dita recursiva quando dentro dela é feita uma ou mais chamadas a ela mesma.
A ideia é dividir um problema original um subproblemas menores de mesma natureza (divisão) e depois combinar as soluções obtidas para gerar a solução do problema original de tamanho maior (conquista). Os subproblemas são resolvidos recursivamente do mesmo modo em função de instâncias menores, até se tornarem problemas triviais que são resolvidos de forma direta, interrompendo a recursão.
Solução 1:
Solução não recursiva.
def fatorial(n):
fat = 1
while n > 1:
fat *= n
n -= 1
return fat
Solução 2:
Solução recursiva: n! = n.(n-1)!

def fatorial(n):
if n == 0: #Caso trivial
return 1 #Solução direta
else:
return n*fatorial(n-1) #Chamada recursiva

Exemplo da sequência:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...A ocorrência da sucessão de Fibonacci na natureza é tão frequente que é difícil acreditar que seja acidental (ex: flores, conchas, mão humana).
Solução 1:
Versão recursiva:
def fibo(n):
if n <= 1:
return n
else:
return fibo(n-1) + fibo(n-2)
Solução 2:
Versão não recursiva:
def fibo(n):
f0 = 0
f1 = 1
for k in range(1,n+1):
f2 = f0 + f1
f0 = f1
f1 = f2
return f0
Análise de eficiência das funções
Fibonacci calculando o número de operações
de soma S(n) realizadas:

Neste caso não faz sentido utilizar a versão recursiva.
Árvore de Recorrência:
A solução recursiva é ineficiente, pois recalcula várias vezes a solução para valores intermediários:
Por exemplo, para F(6)=fibo(6) = 8, temos 2xF(4), 3xF(3), 5xF(2).
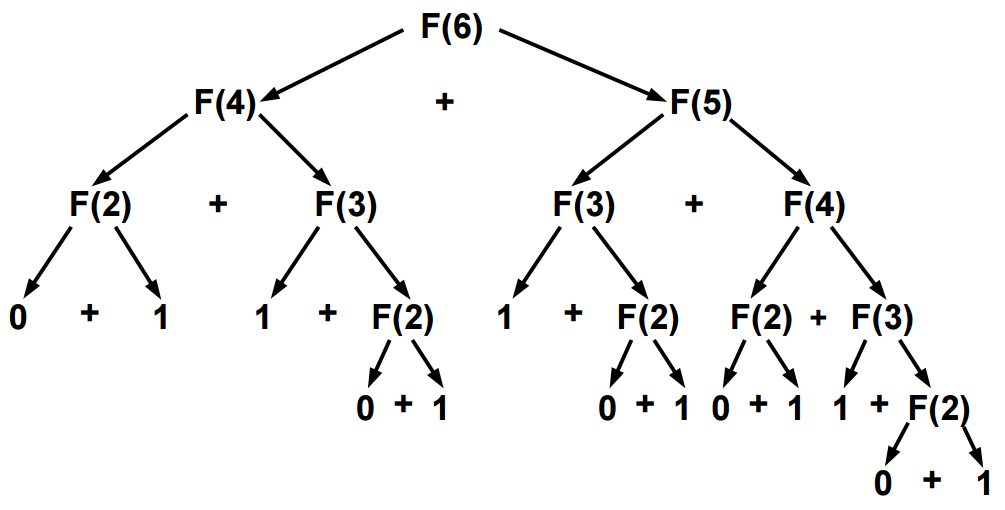
potencia(x, n), que calcule
x elevado a n, sendo x um número real
e n um inteiro positivo.
Solução 1:
Solução não recursiva.
def potencia(x, n):
pot = 1.0
while n > 0:
pot *= x
n -= 1
return pot
Solução 2:
Solução recursiva: x^n = x . x^(n-1)
def potencia(x, n):
if n == 0: #Caso trivial
return 1.0 #Solução direta
else:
return x*potencia(x, n-1) #Chamada recursiva
Solução 3:
Solução recursiva: x^n = x^(n/2). x^(n/2) = (x^(n/2))^2
def potencia(x, n):
if n == 0: #Caso trivial
return 1.0
elif n%2 == 0: #Se n é par...
pot = potencia(x, n//2)
return pot*pot
else: #Se n é ímpar...
pot = potencia(x, n//2)
return pot*pot*x
Solução 1:
Realiza a chamada recursiva em uma cópia de um subtrecho da lista com um elemento a menos, após fatiamento que não copia o último elemento.
def maiorValor(L):
if len(L) == 1:
return L[0]
else:
m = maiorValor(L[:len(L)-1])
if m > L[len(L)-1]:
return m
else:
return L[len(L)-1]
Solução 2:
Realiza a chamada recursiva em uma cópia de um subtrecho da lista com um elemento a menos, após fatiamento que não copia o primeiro elemento.
def maiorValor(L):
if len(L) == 1:
return L[0]
else:
m = maiorValor(L[1:])
if m > L[0]:
return m
else:
return L[0]
Solução 3:
Realiza a chamada recursiva no subtrecho da lista com um elemento a menos,
após a remoção do seu último elemento
via o método pop().
Este último elemento é então posteriormente
reposto na lista a fim de preservar o seu conteúdo original,
através do método append().
def maiorValor(L):
if len(L) == 1:
return L[0]
else:
ult = L.pop()
m = maiorValor(L)
L.append(ult)
if m > ult:
return m
else:
return ult
Solução 4:
Evita o uso de fatiamento de listas e de remoções, usando uma segunda função auxiliar maiorValorAux(L,n) com um parâmetro extra para realizar a recursão.
A função maiorValor(L) passa a ser apenas uma
função de embrulho (wrapper function).
#Encontra o maior valor de uma lista com n elementos.
def maiorValorAux(L, n):
if n==1: #Caso trivial
return L[0]
else:
m = maiorValorAux(L, n-1)
if m > L[n-1]:
return m
else:
return L[n-1]
def maiorValor(L):
n = len(L)
return maiorValorAux(L, n)
Solução 1:
def inverte(L):
n = len(L)
if n > 1:
T = inverte(L[:n-1])
u = L[n-1]
return [u]+T
else:
return L[:]
def main():
L = [1,2,3,4,5]
I = inverte(L)
print(I)
main()
Solução 2:
#Gerar uma copia de L com os elementos invertidos
#de modo recursivo
def inverte(L):
n = len(L)
if n <= 1:
return L[:] #return [ L[0] ] #return list(L)
else:
A = L[0:n-1]
Ainv = inverte(A)
B = [ L[n-1] ]
return B + Ainv
Solução 3:
def inverte2(L):
n = len(L)
if n <= 1:
return L[:] #return [ L[0] ] #return list(L)
else:
A = L[1:n]
Ainv = inverte2(A)
Ainv.append(L[0])
return Ainv
#B = [ L[0] ]
#return Ainv + B
São dados um conjunto de n discos com diferentes tamanhos e
três bases A, B e C.
O problema consiste em imprimir os passos necessários para transferir os discos da base A para a base B, usando a base C como auxiliar, nunca colocando discos maiores sobre menores.
Exemplo:

1º passo: Mover de A para B.
2º passo: Mover de A para C.
3º passo: Mover de B para C.
4º passo: Mover de A para B.
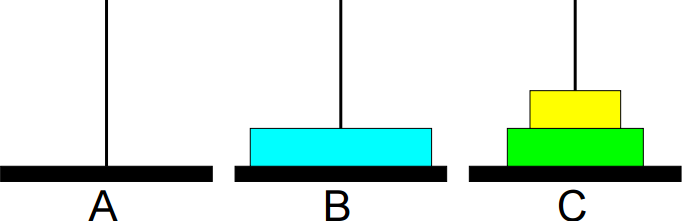
5º passo: Mover de C para A.

6º passo: Mover de C para B.
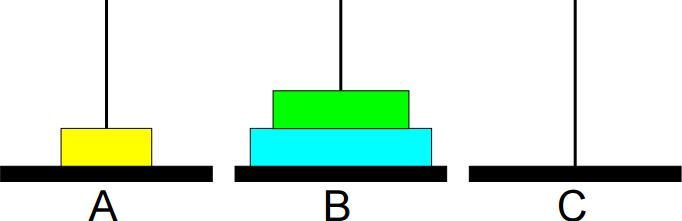
7º passo: Mover de A para B.
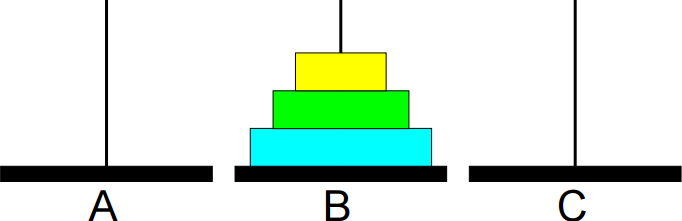
Animação da sequência completa de movimentos:

Solução:
def hanoi(n, orig, dest, aux):
if n == 1:
print("Mover de",orig,"para",dest)
else:
hanoi(n-1, orig, aux, dest)
print("Mover de",orig,"para",dest)
hanoi(n-1, aux, dest, orig)
def main():
n = int(input("Digite a quantidade de discos: "))
hanoi(n, "A", "B", "C")
main()
O número de movimentos necessários para mover n discos é 2n - 1.
n > 0 valores inteiros, em uma lista
L, e um inteiro x, testa se
x pertence à lista.
Solução 1:
Solução por busca exaustiva percorrendo a lista (busca sequencial).
def pertence(x, L):
n = len(L)
i = 0
while i < n:
if L[i] == x:
return True
i += 1
return False
Solução 2:
Essa solução
adiciona na posição seguinte a do último elemento
o valor de x, conseguindo com isso a
simplificação do laço que passa agora a realizar
uma única comparação para cada iteração.
Essa técnica de busca é
conhecida como busca com sentinela.
# busca com sentinela
def pertence(x, L):
n = len(L)
i = 0
L.append(x) #adiciona x no final da lista
while L[i] != x:
i += 1
L.pop() #remove x do final da lista
if i == n:
return False
else:
return True
O algoritmo usado nas duas implementações da função pertence(x,L) acima é chamado de Busca Linear (ou Busca Sequencial). Observe que, nesse algoritmo, toda a lista precisa ser varrida quando o x procurado não está em L.
Mas é possível deixar esse algoritmo mais eficiente quando os elementos da lista na qual se quer buscar um valor estão ordenados, detectando que um elemento não está na lista ordenada mesmo antes de chegar ao seu final. Para isso, basta percorrer os elementos da lista em ordem crescente e encerrar o algoritmo quando x ou um valor maior do que ele for encontrado. Também é possível percorrer os elementos da lista em ordem descrescente; nesse caso, deve-se encerrar o algoritmo quando x ou um valor menor do que for encontrado.
n > 0 valores inteiros ordenados, em uma lista
L, e um inteiro x, testa se
x pertence à lista.
def pertence(x, L):
i = 0
n = len(L)
while i < n and L[i] < x:
i += 1
if i < n and L[i] == x:
return True
else:
return False
Quando a lista está ordenada, a busca pode ser ainda mais eficiente que a descrita acima. Para isso, usamos uma estratégia parecida com a forma como buscamos palavras em um dicionário ou nomes em um catálogo de telefones ou endereços em papel. Nesse caso, ao invés de testar um elemento de cada vez sequencialmente, podemos aplicar o seguinte algoritmo:
Observe que nesse algoritmo, a cada vez que executamos os passos 3 ou 4, metade da lista é eliminada da busca. É por isso que o algoritmo é chamado de Busca Binária.
Para "enxergar" melhor quão mais eficiente a Busca Binária é em relação à Busca Sequencial, considere o seguinte exemplo: procuramos um dado x em uma sequência ordenada com 512 elementos, mas x não está nesta sequência. Antes de indicar que x não está na sequência, o algoritmo de Busca Sequencial precisa testar todos os 512 elementos da sequência. No caso da Busca Binária, o primeiro teste elimina 256 elementos, o segundo 128, o terceiro 64, e depois 32, 16, 8, 4, 2, até que a lista contenha apenas 1 elemento. Dessa forma, ao invés de 512, apenas 9 elementos (ou log(len(L))) precisam ser testados.
Escreva uma função que implemente o algoritmo da Busca Binária. A sua função deve receber como parâmetro uma lista ordenada e um número real x e devolver a posição em que x ocorre na lista ou None caso x não esteja na lista.
# Busca binária:
def pertence(x, L):
n = len(L)
inic = 0
fim = n-1
while inic <= fim:
meio = (inic+fim)//2
if x == L[meio]:
return True
elif x > L[meio]:
inic = meio+1
else:
fim = meio-1
return False
Escreva uma função recursiva que implemente o algoritmo da Busca Binária. A sua função deve receber como parâmetro uma lista ordenada e um número real x e devolver a posição em que x ocorre na lista ou None caso x não esteja na lista.
def pertence_aux(x, L, inic, fim):
meio = (inic+fim)//2
if inic > fim:
return False
elif x == L[meio]:
return True
elif x > L[meio]:
return pertence_aux(x, L, meio+1, fim)
else:
return pertence_aux(x, L, inic, meio-1)
def pertence(x, L):
n = len(L)
inic = 0
fim = n-1
return pertence_aux(x, L, inic, fim)
L com n > 0 números inteiros no intervalo de 0 a 255
(isto é, 0 <= L[i] <= 255 para i = 0,.., n-1),
faça uma função para ordenar os seus elementos em ordem crescente.
Solução
Explorando o fato de que os valores estão em um intervalo limitado de 0 a 255, podemo usar o algoritmo de ordenação do Counting Sort. Para isso vamos usar uma lista de contadores para cada valor de 0 a 255. Portanto, o algoritmo necessita de memória auxiliar.
def ordenacao_por_contagem(L):
n = len(L)
C = [0]*256 #Lista de contadores
for i in range(0,n):
C[L[i]] += 1
#Agora C[k] contém o número de elementos iguais a k.
i = 0
for k in range(0,256):
for c in range(0,C[k]):
L[i] = k
i += 1
Solução 1:
Dividimos ao meio a lista e ordenamos as duas metades via duas chamadas recursivas. A ordenação final é então obtida via intercalação dos valores das duas metades ordenadas.
def mergeSortAux(L, inic, fim):
if fim - inic + 1 <= 1:
return
m = (inic + fim)//2
mergeSortAux(L, inic, m)
mergeSortAux(L, m+1, fim)
A = []
i = inic
j = m+1
while i <= m or j <= fim:
if i > m:
A.append(L[j])
j += 1
elif j > fim:
A.append(L[i])
i += 1
elif L[i] < L[j]:
A.append(L[i])
i += 1
else:
A.append(L[j])
j += 1
for k in range(inic, fim+1):
L[k] = A[k-inic]
def mergeSort(L):
n = len(L)
mergeSortAux(L, 0, n-1)
Exemplo de função principal que chama as
funções anteriores.
def main():
L = [6,3,9,2,7,1,0,4,8,5]
ordenacao_insercao(L)
for i in range(0,n):
print(L[i], end=" ")
print()
x = int(input("Digite x: "))
if pertence(x, L):
print("Sim")
else:
print("Não")
main()