O Cálculo Diferencial e Integral é uma das mais notáveis ferramentas desenvolvidas pelo intelecto humano, sendo capaz de dar conta da descrição da variação de grandezas de diversos tipos. Hoje utilizamos esta teoria como espinha dorsal de diversos ramos das Ciências Exatas, como a Física, as Engenharias e muitas outras.
Enquanto que a Geometria se ocupa do estudo das configurações estáticas, pode-se dizer que o Cálculo se ocupa das configurações "dinâmicas". Não sem motivo, o Cálculo desenvolvido por Sir Isaac Newton surge como ferramenta auxiliar nos seus estudos sobre o movimento.
Empregando as técnicas do Cálculo, somos capazes de calcular grandezas como taxas de variação instantâneas, inclinações de retas tangentes a certas curvas e até mesmo áreas compreendidas entre alguns tipos de curvas e volumes delimitados por diversos sólidos. Vamos analisar, abaixo, o estudo da variação "instantânea" de uma grandeza.
Imagine que certa partícula percorra \(s=s(t)\) unidades de comprimento em \(t\) unidades de tempo. Se desejamos calcular sua velocidade em um instante \(t_0\) (que denotaremos por \(v_{t_0}\)) podemos, um uma primeira abordagem, considerar um pequeno incremento de tempo, , e calcular a velocidade média da partícula entre os instantes \(t_0\) e \(t_0 + \Delta t \):
$$ {v_{t_0} \approx \frac{s(t_0+\Delta t)-s(t_0)}{\Delta t}} $$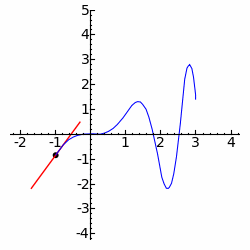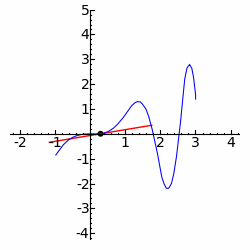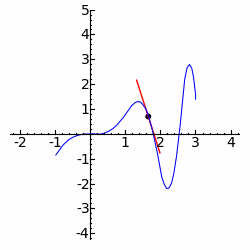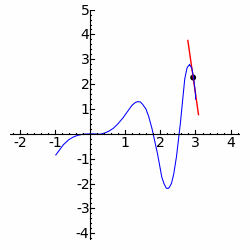
Naturalmente, obteremos aproximações tanto melhores para \(v_{t_0}\) quanto menor for \(\Delta t\). Desta forma, seria extremamente conveniente (e intuitivo), ter à disposição uma grandeza "infinitesimal", ou seja, positiva e infinitamente pequena para obter o valor exato da velocidade instantânea. Segundo KLEINBERG e HENLE (1979), até o início do século XX, era muito comum raciocinar usando este tipo de conceito, que possuía a vantagem de tornar a teoria intuitiva e fácil de compreender. Em seguida apresentamos um exemplo de raciocínio lançando mão daqueles "infinitésimos".
Comecemos introduzindo uma nova grandeza, \(o \), representando uma variação "infinitesimal" (positiva, porém menor do que qualquer outro número positivo) em \(t_0\). A velocidade instantânea será, portanto:
$${v_{t_0}} = \frac{s(t_0+o)-s(t_0)}{o}$$
Digamos, por exemplo, que o movimento de que se trata seja a queda de uma partícula sujeita exclusivamente à aceleração da gravidade, , cuja equação horária do movimento seja 2. A velocidade da partícula no instante 0 será, portanto:
$${v_{t_0}} = \frac{-g\cdot (t_0 + o)^2 - (-g \cdot t_0^2)}{o} = -g \cdot \frac{t_0^2 + 2\cdot t_0 \cdot o + o^2 - t_0^2}{o} =$$ $$= -g \cdot \frac{2t_0 \cdot o + o^2}{o} = -2\cdot g \cdot t_0 - g \cdot o$$Observe que a expressão acima depende de \(o \), o que é absolutamente esperado, uma vez que estamos tirando a taxa de variação média num intervalo de comprimento diferente de zero. No entanto, se \(o\) for se tornando cada vez menor, "fluindo rumo a zero", a taxa variação \(-2gt_0 - g \cdot o\) vai se aproximando cada vez mais de \(-2\cdot g\cdot t_0\), que é a velocidade da partícula no instante \(t_0\). Observe que este valor não depende de \(o\).
Um crítico importante do raciocínio apresentado acima foi o bispo George Berkeley, que argumentava que não fazia sentido argumentar a existência de uma grandeza pequena, , que ora é considerada diferente de zero (nos denominadores) e, no final, considerada igual a zero. Berkeley publicou suas críticas em 1734 no panfleto intitulado "O analista: ou um discurso endereçado a um matemático infiel". Somente na segunda metade do século XIX foi que o matemático alemão Karl Weierstrass pôde introduzir o conceito formal de limite, em sua contextura atual, permitindo que o Cálculo prescindisse, definitivamente, das grandezas infinitesimais.
Munidos da definição exata de limites, podemos apresentar de modo super preciso conceitos como o da continuidade de uma função em um ponto, o da derivada e da integral definida de funções "suficientemente" bem comportadas.
Para além do estudo das variações, o Cálculo nos permite, também, calcular "somas" de grandezas contínuas, justificando, por exemplo, o método dos indivisíveis de Cavalieri. Com suas ferramentas (como a integral de Riemann), podemos calcular áreas e volumes delimitados pelas mais diversas curvas e superfícies.
O cálculo é usado em todos os ramos das ciências físicas, na ciência da computação, estatística, engenharia, economia, medicina e em outras áreas sempre que um problema possa ser modelado matematicamente e uma solução ótima é desejada, ele é um estudo mais profundo de funções. [WIKIPEDIA (2020)]
O Cálculo é oriundo de questões tanto da Matemática Pura quanto da Matemática Aplicada [STEWART (2013)], e seus antecedentes remontam aos tempos de Arquimedes. Dentre os gigantes que precederam o desenvolvimento do Cálculo como o conhecemos hoje, se encontram John Wallis, Pierre de Fermat, Galileu Galilei e Johannes Kepler,
Wallis, em 1656, publicou seu livro Aritmetica Infinitorum ("Aritmética do infinito"). Fermat, em 1679, publicava seu livro De Tangentibus Linearum Curvarum ("De tangentes de linhas curvas"), onde apresentava seu método de achar retas tangentes a curvas - um problema estreitamente ligado ao Cálculo. Kepler, por sua vez, formulou suas três leis básicas do movimento planetário, dando subsídio para que Isaac Newton formulasse sua Lei da Gravitação Universal. Os parágrafos a seguir foram extraídos da Wikipedia:
Coube a Gottfried Wilhelm Leibniz e a Isaac Newton recolher essas ideias e juntá-las em um corpo teórico que viria a constituir o cálculo. A ambos é atribuída a simultânea e independente invenção do cálculo. Leibnitz foi originalmente acusado de plagiar os trabalhos não publicados de Isaac Newton; hoje, porém, é considerado o inventor do cálculo, juntamente com Newton. Historicamente Newton foi o primeiro a aplicar o cálculo à física ao passo que Leibniz desenvolveu a notação utilizada até os dias de hoje, a notação de Leibniz. O argumento histórico para conferir aos dois a invenção do cálculo é que ambos chegaram de maneiras distintas ao Teorema Fundamental do Cálculo,
$${\int_{a}^{b}f(x)dx = F(b)-F(a)}$$Quando Newton e Leibniz publicaram seus resultados, houve uma grande controvérsia de qual matemático (e portanto que país: Inglaterra ou Alemanha) merecia o crédito. Newton derivou seus resultados primeiro, mas Leibniz publicou primeiro. Newton argumentou que Leibniz roubou ideias de seus escritos não publicados, que Newton à época compartilhara com alguns poucos membros da Sociedade Real. Esta controvérsia dividiu os matemáticos ingleses dos matemáticos alemães por muitos anos. Um exame cuidadoso dos escritos de Leibniz e Newton mostra que ambos chegaram a seus resultados independentemente, com Leibniz iniciando com integração e Newton com diferenciação. Nos dias de hoje tem-se que Newton e Leibniz descobriram o cálculo independentemente. Leibniz, porém, foi quem deu o nome cálculo à nova disciplina, Newton a chamara de "A ciência dos fluxos".
Relações planas. Representação geométrica. Produto cartesiano e relações. Domínio, contradomínio, imagem e gráfico de uma relação. Univocidade e totalidade de uma relação. Funções. Funções de uma variável real a valores reais. Preservação e inversão da ordem. Paridade de uma função. Funções definidas por partes. Translações no gráfico de uma função. Funções limitadas e funções periódicas. Injetividade, sobrejetividade e bijetividade. Operações com funções. Inversas laterais de uma função: seções e retrações. A inversa de uma função.
Funções Trigonométricas Diretas: Seno e Cosseno; Estudo de Variações das Funções Trigonométricas Seno e Cosseno; Funções Trigonométricas Diretas: Tangente, Cotangente, Secante e Cossecante; Funções Trigonométricas Inversas (ou “Funções Ciclométricas”); Modelagem usando as Funções Seno e Cosseno;
Funções exponenciais: motivação e exemplos; Crescimento e decaimento exponencial; Variações das funções exponenciais; Número e: motivação e definição; Irracionalidade do número e; Logaritmos: motivação histórica; Funções logarítmicas; Propriedades das funções logarítmicas deduzidas pelo método axiomático.
Sequências e subsequências; Definição de limite de uma sequência; Definição de soma e de produto de sequências por escalar; Propriedades; Sequências crescentes e decrescentes; Unicidade do limite de uma sequência; Vizinhança (ou entorno) de um ponto: vizinhanças completas e laterais; Ponto de acumulação. Ponto de acumulação lateral. Limites superior e inferior de uma função; Existência de ponto de acumulação: o Teorema de Bolzano-Weierstrass. Definição formal do número e.
Definição formal de limite via épsilons e deltas; Propriedades Aritméticas dos Limites; Definição de limites laterais; Unicidade do limite no caso de sua existência; "O" Teorema
Definição de continuidade de uma função; Definição de função descontínua em um ponto; Propriedades "aritméticas" das funções contínuas; Teorema da Conservação do Sinal; Exemplos de Funções Contínuas; Cálculo de alguns limites.
Mudança de variável na resolução de limites; Extensões do conceito de limite: limites "infinito e menos infinito"; Extensões do conceito de limite: limites laterais "infinito e menos infinito"; Extensões do conceito de limite: limites no "infinito e menos infinito"; Extensões do conceito de limite: limites "infinito e menos infinito" no "infinito e em menos infinito"; Propriedades "operatórias" de limites infinitos e no infinito; Limites no infinito de funções racionais; Cálculo de alguns limites.
O Teorema do Confronto; O Teorema do Confronto para limites laterais à direita; O Teorema do Confronto para limites laterais à esquerda; O Teorema do Confronto para limites no infinito; Funções infinitésimas em um ponto; Produto de uma função infinitésima por uma função limitada em um ponto; Limite trigonométrico fundamental: \({\lim_{x \to 0} \frac{\sin(x)}{x}} = 1\); Limite exponencial fundamental: \({\lim_{x \to \infty} \left(1+\frac{1}{x}\right)^x = e}\); Propriedades de Funções Contínuas; O Teorema do Anulamento; O Teorema do Valor Intermediário; O Teorema da Limitação; O Teorema de Weierstrass.
Derivadas. Motivação cinemática; Declividade de uma curva; Derivadas; Derivadas laterais; Derivabilidade e Continuidade; Curvas sem tangentes e movimento browniano; Regras de derivação: derivação da soma, diferença, produto e quociente de funções; Regra da cadeia;
Funções elementares e suas derivadas; - Derivada da função seno; - Derivada da função cosseno; - Derivada da função \( x \mapsto x^n\) com \(n \in \mathbb{Z}\); - Derivada da função exponencial de base \(a \in ]0,1[\cup ]1,\infty[\); - Derivada da função logarítmica; - Derivada da função \(x \mapsto x^{\alpha}\) com \(\alpha \in \mathbb{R}\setminus \mathbb{Q}.\); - Cálculo de algumas derivadas; - Funções definidas implicitamente por equações; - Derivação de funções dadas implicitamente; - Derivação da função inversa.
Aplicações da Derivada: Regra de L'Hospital; Aplicações da Derivada: Intervalos de crescimento e de decrescimento de uma função; Aplicações da derivada: determinação de extremantes globais; Taxa de variação pontual; O Teorema do Valor Médio; O teste da Derivada Primeira.
Derivadas de ordem superior; A interpretação cinemática da derivada segunda; A concavidade do gráfico de uma função; O teste da derivada segunda; Máximos e mínimos de uma função contínua em um intervalo; Assíntotas do gráfico de uma função; Esboço do gráfico de funções;
Motivação para a integração: área delimitada pela parábola \(y=x^2\), pela reta \(x=1\) e pelos eixos coordenados; A integral de Riemann; Partições de um intervalo; Integrabilidade de funções contínuas; Linearidade da Integral de Riemann; Monotonicidade da Integral de Riemann; Aditividade da Integral de Riemann; O Teorema da Média; O Teorema Fundamental do Cálculo - parte 1; Primitiva de uma função; O Teorema Fundamental do Cálculo - parte 2; Propriedades das integrais indefinidas; O Teorema da Mudança de Variável; Apêndice: rudimentos da teoria da integração segundo Riemann.
Método da mudança de variável (ou substituição); Método da integração por partes; Frações racionais, frações racionais parciais e sua integração; Integração de frações racionais; Integração de certas classes de funções trigonométricas; Integração de produtos de potências de funções trigonométricas; Integração de expressões da forma \(R(x, \sqrt{k \pm x^2})\): Integrais da forma: \(\int R(x, ax^2+bx+c)dx\); Funções cujas integrais não podem ser expressas em termos de funções elementares.
Linearização e diferenciabilidade; Interpretação de dy/dx enquanto um quociente; Diferencial de uma função em um ponto; Variações absoluta, relativa e percentual; Erro na aproximação diferencial; Fórmula de Taylor; Estimativa do erro.
Equações diferenciais ordinárias; Problema de valor inicial; Resolução de EDOs de variável separável; Resolução de EDOs homogêneas; Resolução de EDOs lineares de primeira ordem (fator integrante); Resolução de EDOs de Bernoulli; Aplicações.
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA
UNIVERSIDADE DE SÃO PAULO
Rua do Matão, 1010 - CEP 05508-090 - São Paulo - SP
Telefone: (11) 3091-6193 E-mail: j.berni@unesp.br