Sejam todes bem vindes ao curso de Cálculo IV! Neste curso vamos aumentar ainda mais o nosso repertório matemático estudando diversos conceitos como séries numéricas, séries de potências reais e complexas. Derivação e integração termo a termo. Funções elementares. Derivação complexa, integração complexa, fórmula de Cauchy, fórmula integral para as derivadas. Teorema do máximo módulo, teorema de Liouville, singularidades e resíduos.
Começamos este curso estudando sequências e séries de números reais. Posteriormente, estudaremos sequências e séries complexas (conforme a animação a seguir), em que se ilustra o conceito de convergência de uma sequência de números complexos, \((z_n)_{n \in \mathbb{N}}\) para um dado número complexo, \(z\), representado como o centro do disco avermelhado abaixo. Por exemplo, diremos que \(\lim_{n \to \infty} z_n = z\) se, dado qualquer \(\varepsilon>0\), formos capazes de exibir um índice (na animação seria o \(n_0 = 25\)) a partir do qual todos os termos da sequência estão dentro do disco centrado em \(z\) e com raio \(\varepsilon\).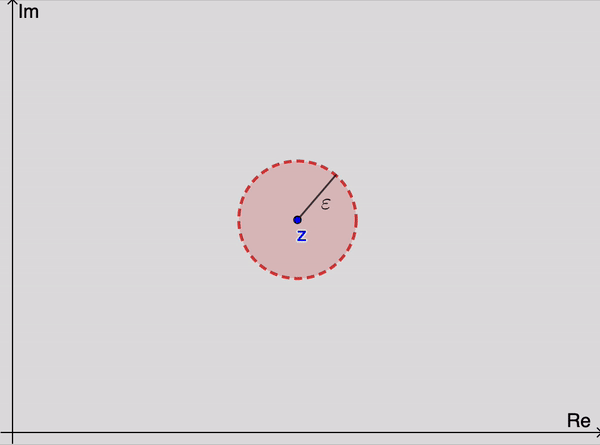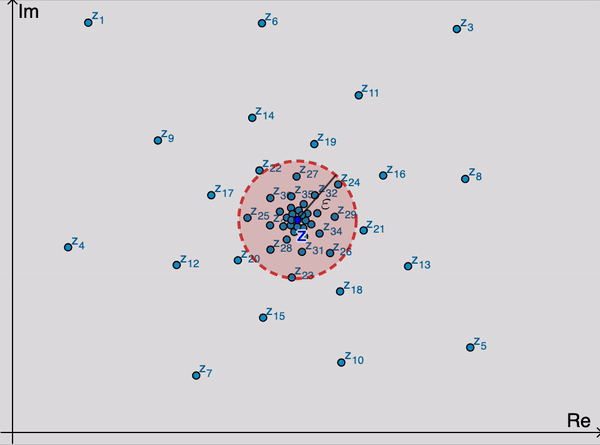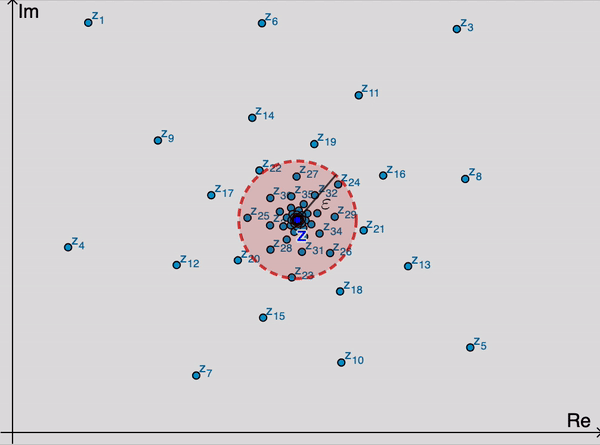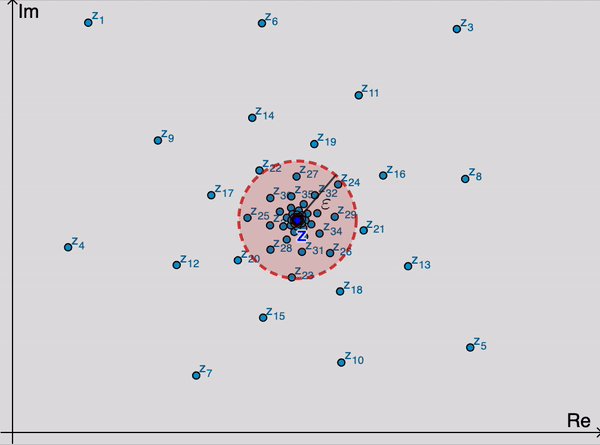
Posteriormente, estudaremos o conceito de diferenciabilidade para funções de uma variável complexa (que, embora similar à derivabilidade de funções de variáveis reais a valores reais, tem diversas particularidades). Abaixo verifica-se uma ilustração dos diversos "caminhos" pelos quais podemos nos aproximar de um ponto, \(z_0\), do domínio de uma função \(f: \Omega \subset \mathbb{C} \to \mathbb{C}\).
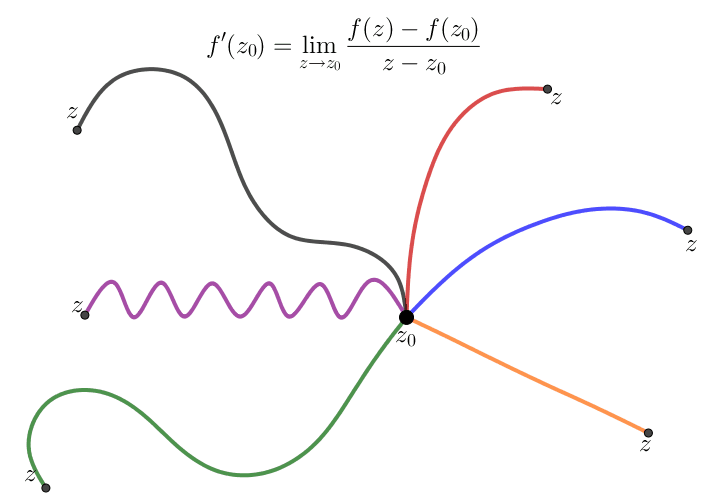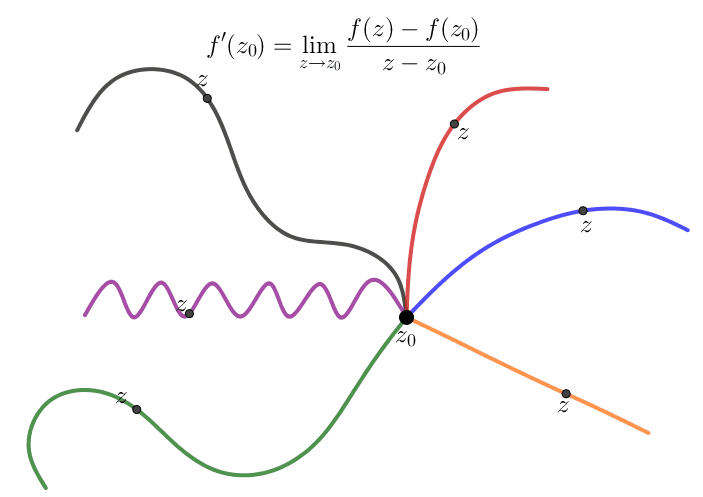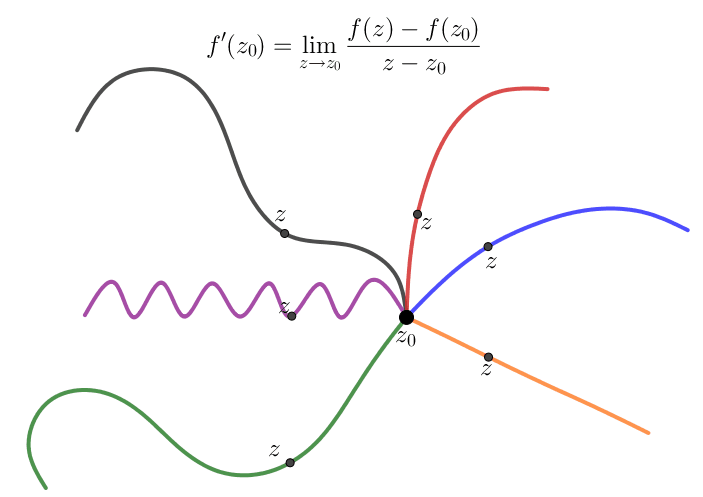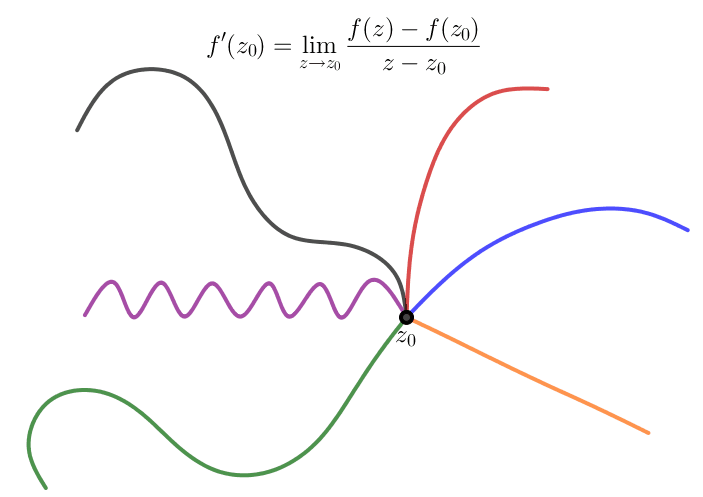
| Dia | Horário |
|---|---|
| Terça-feira | 08h00 às 10h00 ✔ |
| Quinta-feira | 10h00 às 12h00 ✔ |
| Atividade | Entrega |
|---|---|
| Lista sobre convergência de sequências e séries numéricas | 26/9/2024 ✔ |
| Avaliação de Aprendizagem 2 | 28/11/2024 |
Sequências de números reais: conceito e definições. Convergência e divergência de uma sequência de números reais. Subsequência de uma sequência de números reais. Propriedades do limite de uma sequência numérica. Sequências crescentes e decrescentes. Teorema da Conservação do Sinal. Conceito de sequência de Cauchy. Sequências limitadas. Toda sequência de Cauchy é convergente. Apêndice: o número \(e\).
Séries numéricas: série geométrica e série telescópica. Propriedades dos limites de séries numéricas. Condição necessária para a convergência de uma série numérica. Critério do termo geral para divergência de uma série numérica. Critérios de convergência: Critério da Comparação, Teste da Integral para a convergência e para a divergência. Critério da Comparação no Limite. Teste da Razão (D'Alembert) e Teste da Raiz (Cauchy).
Sequências e séries de funções. Séries de potências. Raio e intervalo de convergência de uma série de potências. Continuidade, derivabilidade e integrabilidade de uma função definida por uma série de potências. Operações "aritméticas" com séries de potências. Funções analíticas e expansão de uma função em série de potências.
Números complexos: breve relato histórico (relação com a equação cúbica). \(\mathbb{C}\) enquanto conjunto de pares ordenados de números reais. \(\mathbb{C}\) enquanto corpo. Operações com números complexos. Forma trigonométrica de um número complexo. Noções topológicas do plano complexo. Curvas no plano complexo. Limites de funções de uma variável complexa a valores complexos. Funções complexas limitadas. Continuidade e compacidade. Sequências de números complexos: sequências de Cauchy. Completude de \(\mathbb{C}\). O Teorema da Limitação do Módulo. Funções holomorfas. Propriedades das funções complexas diferenciáveis e as Condições de Cauchy-Riemann. A Regra da Cadeia. Funções harmônicas.
Integração de funções complexas. Singularidades. Resíduos. Teorema de Morera. Teorema de Cauchy. Teorema de Liouville. Cálculo de integrais impróprias usando resíduos,
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA
UNIVERSIDADE DE SÃO PAULO
Rua do Matão, 1010 - CEP 05508-090 - São Paulo - SP
Telefone: (11) 3091-6193 E-mail: jeancb@ime.usp.br