Geometrias Euclidiana e
Não-Euclidiana

Geometrias Euclidiana e
Não-Euclidiana

Pares de retas com um ponto em comum que são paralelas a uma terceira!
A soma dos ângulos interiores do triângulo é menor que 180 graus!
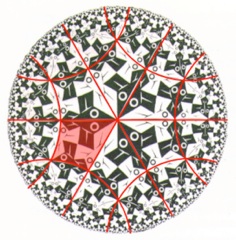
Descrição: A Geometria Euclidiana consiste num sistema de axiomas “bastante” naturais. O mais importante deste axiomas é o postulado das paralelas: Dada uma reta L e um ponto fora desta reta, existe uma única reta R passando por este ponto e que não intersecta a reta L. Na primeira parte deste curso estudaremos a Geometria Euclidiana Afim usando conceitos modernos de matemática (Teoria de grupos, Álgebra linear) que permitem entender as simetrias nesta geometria. Posteriormente, veremos vários exemplos de geometrias onde o postulado das paralelas não vale (veja as figuras acima), isto é, geometrias não-Euclidianas. Os modelos de geometrias não-Euclidianas que abordaremos nesta disciplina são: Geometria projetiva, Geometria esférica e Geometria Hiperbólica.
Porquê estudar Geometria Não-Euclidiana?
Porque é fonte de exemplos matematicamente bonitos! Além disso, a Geometria Não-Euclidiana Hiperbólica teve um impacto enorme na matemática atual, tendo aplicações em: variáveis complexas, funções automorfas, topologia em dimensão 3 (Conjectura de Geometrização de Thurston), Relatividade, e muito mais...
Pré-requisitos: Conhecimento de Teoria de Grupos e Álgebra Linear.
Aulas: Segundas e Quartas 17:30-19:30 no Anfiteatro A do Centro Politéctnico.
ATENÇÃO: Na semana 23-27 de Maio, as aulas serão ministradas pelo Prof. Edson Ribeiro.
Avaliação: Três provas cujas datas são:
Prova 1: 04/05/2011
Prova 2: 06/06/2011
Prova 3: 20/06/2011
Segunda Chamada: 22/06/2011
Exame Final: 06/07/2011
A nota final será a média aritmética das três provas. Não haverá prova substitutiva.
Ementa: Os tópicos que estudaremos incluem:
1. Geometria Afim: Espaço Afim, Transformações afins, Exemplos. Isometrias, órbitas e grupos de isotropia.
2. Geometria Esférica: A esfera de dimensão 2, triângulos esféricos, Fórmula de Girard, Poliedros regulares e suas simetrias, Fórmula de Euler.
3. Geometria Projetiva: Espaço Projetivo, Topologia do Espaço Projetivo, Transformações projetivas, Razão cruzada, Isometrias.
4. Geometria Hiperbólica: Modelos da geometria hiperbólica, Semi-plano, Disco de Poincaré, Modelo de Lorentz. Isometrias hiperbólicas.
Referências:
 P. Ryan, Euclidean and Non-Euclidean Geometry: an analytic approach.
P. Ryan, Euclidean and Non-Euclidean Geometry: an analytic approach.
 M. Audin, Geometry.
M. Audin, Geometry.
 H.S.M. Coxeter, Introduction to Geometry.
H.S.M. Coxeter, Introduction to Geometry.
Listas:
1. Lista1.pdf
2. Lista2.pdf
3. lista3.pdf
4. Lista4.pdf
5. Lista5.pdf